... Hermione was pulling her wand out of her bag.
It might be invisible ink!she whispered.She tapped the diary three times and said,
Aparecium!— J. K. Rowling, Harry Potter and the Chamber of Secrets
Introduction
This paper introduces Aparecium, a library intended to make
the use of invisible XML
convenient for users of
XSLT and XQuery. This introduction provides some background
information on invisible XML and describes the purpose of the
Aparecium library. The next section illustrates the use of the
library with a sample application to parse and evaluate arithmetic
expressions (section “A sample application”). Following that
illustration the library's public interface is described and some
technical issues are discussed. The paper concludes with a survey
of related work (section “Related work”) and a section on
future tasks (section “Future work”).
Invisible XML
In 2013, Steven Pemberton introduced an idea he called
invisible XML
(Pemberton 2013),
which he describes as a method for treating non-XML
documents as if they were XML
(Pemberton 2019b). More recently, he has produced
a more formal specification of the idea (Pemberton 2019a). From a data creator's or author's point
of view, invisible XML (ixml, for short) allows authors to use
formats other than XML if they prefer, while still retaining
access to the XML tool chain. From the XML programmer's point
of view, it allows people working within the XML eco-system to
have more convenient access to non-XML data. The only
prerequisite is that it must be possible to describe the data
using a context-free grammar.
A great many resources are available in specialized formats like CSS, wiki markup, or domain-specific notations. Social-science data may interleave group-level records with individual-level records in a way that varies from project to project. Other resources are distributed in generic non-XML formats like comma-separated values or JSON. Nor is it only entire documents, files, or web resources which may use non-XML formats. SGML and XML documents have a long history of including elements or attributes whose value is written in a specialized notation: mathematical expressions are often written in TeX or LaTeX; pointers may be written as URLs, as other forms of URI, as ISSNs or ISBNs, or (not too long ago) in TEI extended-pointer notation; inline styles are now frequently written in CSS. All of these notations make visible some of the structure of the information; sometimes it would be convenient to have easy access to that structure in XML processing. Invisible XML is a way of making that possible.
Context-free grammars and parse trees
The main requirement of invisible XML is that the non-XML
data to be read should be described by a context-free grammar.
(Readers not familiar with this concept may think of it as a
kind of DTD or schema for non-XML data.) For example, we might
describe the language of arithmetic expressions like 23 *
(2 + 7.2)
with the following grammar, written in ixml
notation:
{ An expression is the sum of one or more terms. }
expression: term, (add-op, term)*.
{ A term is the product of one or more factors. }
term: factor, (mul-op, factor)*.
{ Addition operators and multiplication operators are
+, -, *, and /. }
add-op: "+"; "-".
mul-op: "*"; "/".
{ A factor is either a number or a parenthesized
sub-expression. }
factor: number; "(", expression, ")".
number: digit+, (".", digit*)?.
Here, braces surround comments, each rule of the grammar
consists of a single non-terminal symbol followed by a colon, a
regular expression on the right-hand side of the colon, and a
full stop. On the right hand side, quoted strings denote
terminal symbols, unquoted identifiers are non-terminal symbols,
commas separate items which must appear in sequence, semicolons
separate alternatives, parentheses enforce grouping when
necessary, question mark signals that the immediately preceding
expression is optional, plus that it may occur one or more
times, and asterisk that it can occur zero or more times.
Parsed against the grammar above, the arithmetic
expression Figure 123 + 1834 / (60 - 3) - 9
has a parse
tree of the form
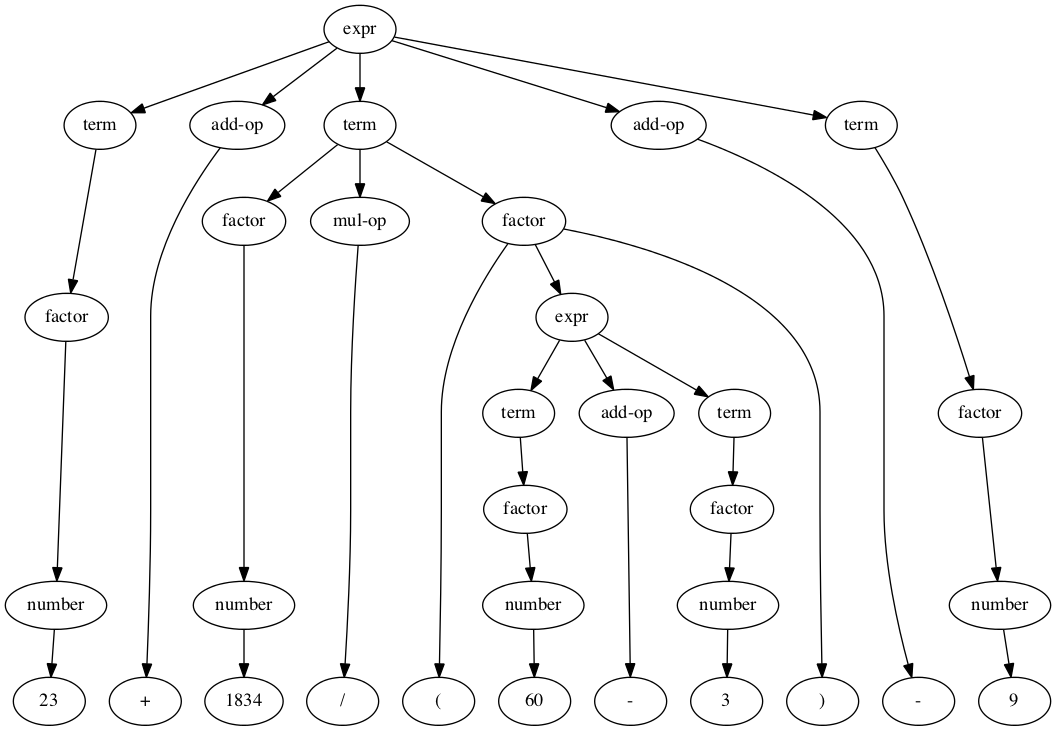
It will not have escaped the reader that such a tree structure can readily be expressed in an XML document:
<expr>
<term>
<factor>
<number>23</number>
</factor>
</term>
<add-op>+</add-op>
<term>
<factor>
<number>1834</number>
</factor>
<mul-op>/</mul-op>
<factor>
<expr>
<term>
<factor>
<number>60</number>
</factor>
</term>
<add-op>-</add-op>
<term>
<factor>
<number>3</number>
</factor>
</term>
</expr>
</factor>
</term>
<add-op>-</add-op>
<term>
<factor>
<number>9</number>
</factor>
</term>
</expr>
Such deeply-nested tree structures and such a high
markup-to-content ratio are unusual in XML vocabularies
designed for hand authoring, but they can when well designed
make processing the information much simpler.[1] For example, it
should be fairly easy to see that an XSLT stylesheet is capable
not just of displaying but of evaluating arithmetic expressions
represented in this way. Each node in the syntax tree which
represents a well-formed (sub)expression can be assigned a
value. For leaf nodes containing numerals, the value is the
number denoted by the numeral. Leaf nodes denoting operators and
whitespace are not well formed arithmetic expressions and have
no numeric value. In the case of factors, terms, and
expressions, the value depends on the values of their children,
in the pattern known as compositional
semantics (the meaning of the compound expression is
composed from the meanings of its component
parts). If we label each node with its value, the syntax tree
looks like this:
Figure 2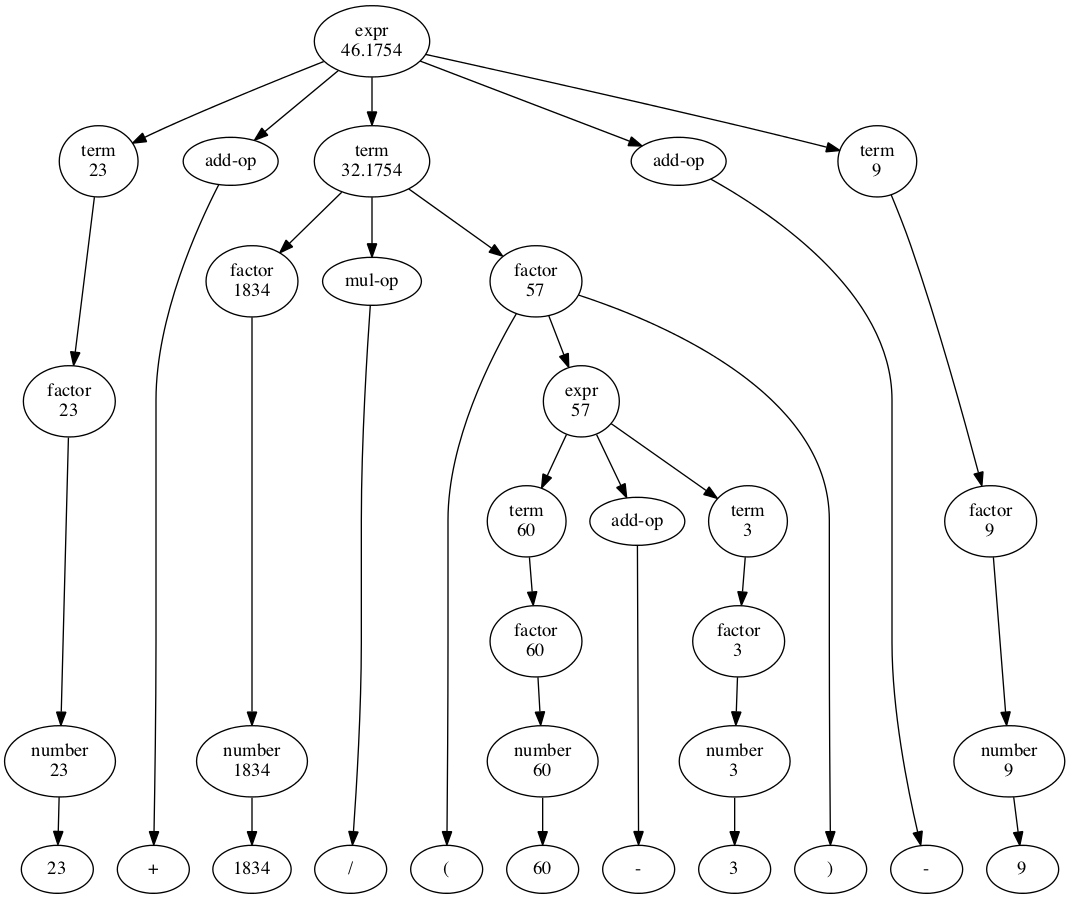
In a nutshell, the idea of invisible XML is to regard the XML structure as latent in the original expression: present, but invisible. The task of Aparecium or any other invisible-XML parser is to make that invisible XML visible, so that it can be processed by standard XML tools.
Earley parsers
Many tools for using context-free grammars require that the grammar have particular properties which are necessary for particular parsing strategies to work: some tools require that the grammar be (as computer scientists say) LL(1), or LL(k); others like the classic parser generator yacc require that the grammar be LALR(1). I will not detain the reader with a description of what these different properties entail, or even what the abbreviations mean; suffice it to say that not all context-free grammars satisfy the constraints.
The advantage of such restrictions is that they allow the tool to use parsing techniques which are relatively simple, require relatively little storage, and are relatively fast. The disadvantage is that even experienced parser writers may find it difficult to write grammars which satisfy the constraints, and for existing notations such grammars may not even be possible. Worse, it is very difficult to explain to users of the tool even what the constraints are, without administering a short course in the relevant parsing algorithms.[2]
Invisible XML takes a different approach: users are not required to supply grammars that satisfy any particular set of implementation-related constraints. Instead, implementations are required to accept any context-free grammar. This in turn suggests that implementations will need to use one of the algorithms which is guaranteed to work for all context-free grammars without restriction. There are several such algorithms[3], but the invisible XML specification suggests the use of an Earley parser.
Earley parsers are guaranteed to handle arbitrary context-free grammars, including ambiguous ones. In the worst case they parse an input in time and space proportional to the cube of the length of the input, but on non-pathological grammars their performance is much closer to being linear in the length of the input. They will still however typically be slower than non-general parsers, because they have more housekeeping overhead. Issues arising in the use of functional languages like XQuery or XSLT to implement Earley parsing, and the extension of the algorithm to cover regular-right-part grammars (like invisible XML) instead of only grammars in Backus-Naur Form, have been discussed in general terms by Sperberg-McQueen 2017.
The Aparecium library
Pemberton's original description of invisible XML proposes
that those who publish resources parseable by means of invisible
XML should label them with the MIME type
application/xml and including a link to the
appropriate invisible-XML grammar in the HTTP header (Pemberton 2013). When the HTTP server is configured
as proposed, a CSS stylesheet can be served both as
text/css and as
application/xml-invisible; content negotiation
between the client and the server will determine which form is
sent. When the client's request specifies a preference for the
application/xml form, the server will serve the stylesheet as
usual, but instead of the line
Content-Type: text/css
the HTTP header will include the line
Content-Type: application/xml-invisible;
syntax=http://example.com/syntax/css.ixml
The syntax parameter allows suitably designed
software on the client side to fetch the ixml grammar for
the resource from the specified location, use it to parse
the resource, and present the resource to the user in an XML
form.
This design allows invisible XML to fit neatly into the architecture of the Web, but for the moment it has a certain flaw. Most of the non-XML resources which we might like to process as XML are served only in their default MIME type, not as application/xml.
The Aparecium library is intended to make it easy for people working in XSLT or XQuery to use invisible XML without requiring any cooperation from webmasters or servers belonging to other organizations. It does not rely on distant servers to label resources with the application/xml MIME type, although if they do, it can handle those cases, too.
For resources served as described by Pemberton 2013, Aparecium offers a call modeled on
the doc() function of XPath 2.0: a call to
aparecium:doc($uri)
will (in the normal case) return an XML representation of
the resource at the URI given.
For resources not served in this way, Aparecium offers a way for the XSLT or XQuery programmer to take matters into their own hands by specifying both the URI of the resource to retrieve and the URI of an ixml grammar describing it:
aparecium:parse-resource($uriR, $uriG)
When the non-XML material and its grammar are not on the Web or in files but are available in string form, Aparecium offers a similar function to parse a string:
aparecium:parse-string($string, $grammar)
Since ixml grammars are themselves described by an ixml
grammar, they also have a defined XML representation, so the
grammar can also be supplied by the user in XML form; this
saves parsing the grammar into XML preparatory to parsing
the resource the user is interested in. Given the XML form
of a grammar, Aparecium pre-processes it before using it to
parse input; this pre-processed form can also be used. A
family of functions is provided to allow various
combinations of these variations: input as URI or string;
grammar as URI or as string or as
standard
XML or as pre-processed
XML.
A sample application
As a simple application of Aparecium, let us consider an evaluator for arithmetic expressions.
The ixml grammar for the expressions we would like to accept is similar to the one given above, but extended in a few ways: we allow whitespace to appear within expressions; we predefine two named constants; and we allow some alternative Unicode forms for symbols and constants.
{ arith.ixml: a simple language for four-function
arithmetic expressions. }
expression: term, (s, addop, s, term)*.
term: factor, (s, mulop, s, factor)*.
factor: number;
constant;
"(", s, expression, s, ")".
addop: "+"; "-".
mulop: [ "*"; #B7; #D7; "/"; #F7 ].
{ B7 = middle dot, D7 multiplication symbol, F7 division symbol. }
number: decimalnumber, exponent?.
decimalnumber: sign?, digit+, (decimalpoint, digit*)?;
decimalpoint, digit+.
-decimalpoint: ".".
-sign: ["-"; "+"].
exponent: ("e"; "E"), sign?, digit+.
-digit: ["0"-"9"].
-s: [#20; #0A; #0D; #09]*.
constant: "pi"; "e"; [ #3C0 ].
{ #3C0 is pi }
Expressions we would like to accept include:
-
1 + 3 - 2
-
1 * 2 - 10 / 2
-
1 * (2 - 10) / 2
-
1.02e3 + 3
-
π * 20
Expressions we would like to reject (ideally with useful diagnostics, though that is not the case at the moment) include:
-
1 + 3 2
-
1 * 2 +- 10 / 2
-
1 * (2 = 10) / 2
-
1.02e3 + 3
-
π × 42^2
-
r = 42; π × r^2
The application will allow the user to type in an arithmetic expression and produce an XML representation of the parse tree. For example, we can type in the expression mentioned above into the text window:
Figure 3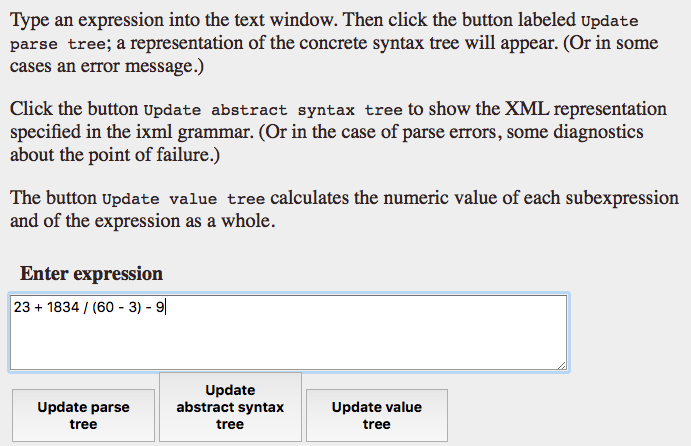
When the user clicks on the appropriate buttons, the expression is parsed and the XML representation already shown above is displayed.
Note
Note: For pedagogical purposes, the
demo application produces not only the
abstract
syntax tree specified in the
ixml grammar, but also a raw
or
concrete
parse tree which represents
all non-terminal symbols as elements, eliding none and
representing none of them as attributes. Such behavior
is unlikely to be of interest except to those interested
in parser implementation.
To illustrate the possible exploitation of the XML structure, the application also provides a button to find the numeric value of the expression. To make it easier (possibly) to understand the evaluation process, the values of all subexpressions in the tree are also shown:
<expression value="46.1754385964912">
<term value="23">
<factor value="23">
<number value="23">
<decimalnumber value="23"/>
</number>
</factor>
</term>
<addop>+</addop>
<term value="32.1754385964912">
<factor value="1834">
<number value="1834">
<decimalnumber value="1834"/>
</number>
</factor>
<mulop>/</mulop>
<factor value="57">
<expression value="57">
<term value="60">
<factor value="60">
<number value="60">
<decimalnumber value="60"/>
</number>
</factor>
</term>
<addop>-</addop>
<term value="3">
<factor value="3">
<number value="3">
<decimalnumber value="3"/>
</number>
</factor>
</term>
</expression>
</factor>
</term>
<addop>-</addop>
<term value="9">
<factor value="9">
<number value="9">
<decimalnumber value="9"/>
</number>
</factor>
</term>
</expression>
The internals of the demo application are not of great interest except as they illustrate the use of the Aparecium library. The user interface is provided by an XForm displayed by a web browser, which sends the expression typed by the user to the server and accepts the XML representation of the expression's parse tree in return. The actual parsing takes place on the server (although it could in principle be performed in the browser using an implementation of XQuery or XSLT 3.0 in the browser). The arithmetic evaluation of the expression is handled by an XSLT 1.0 stylesheet running in the browser, the only non-trivial part of which are the templates to calculate the values of expressions and terms, which requires coping with an indeterminate number of child expressions and applying the specified operators in the appropriate left-to-right sequence.
The part of the application of most concern for purposes of
this paper is the XQuery module that turns a string containing
an arithmetic expression into an XML document representing its
parse tree. In this case, it could consist essentially of a
single call to the Aparecium parse-string()
function, like this:[4]
declare variable $expression as xs:string external;
import namespace a = "http://blackmesatech.com/2019/iXML/Aparecium";
a:parse-string(
$expression,
unparsed-text(
"http://blackmesatech.com/2019/demos/arith/arith.ixml"
)
)
To explain why this is not the way the demo application is
actually implemented will require a short discussion of some
of the internal organization of the library.
Ignoring the fact that at various times things
move from one machine to another, the overall flow of
the application is as shown in this diagram:
Figure 4 Figure 5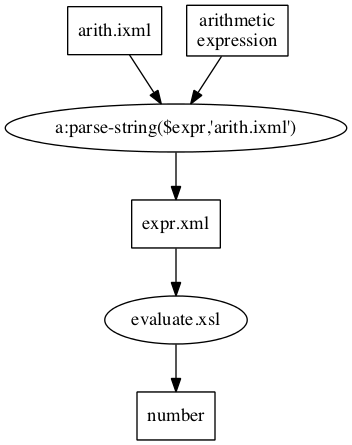
parse-resource(), however, the grammar
goes through several transformations, as shown in this
expansion of the diagram:
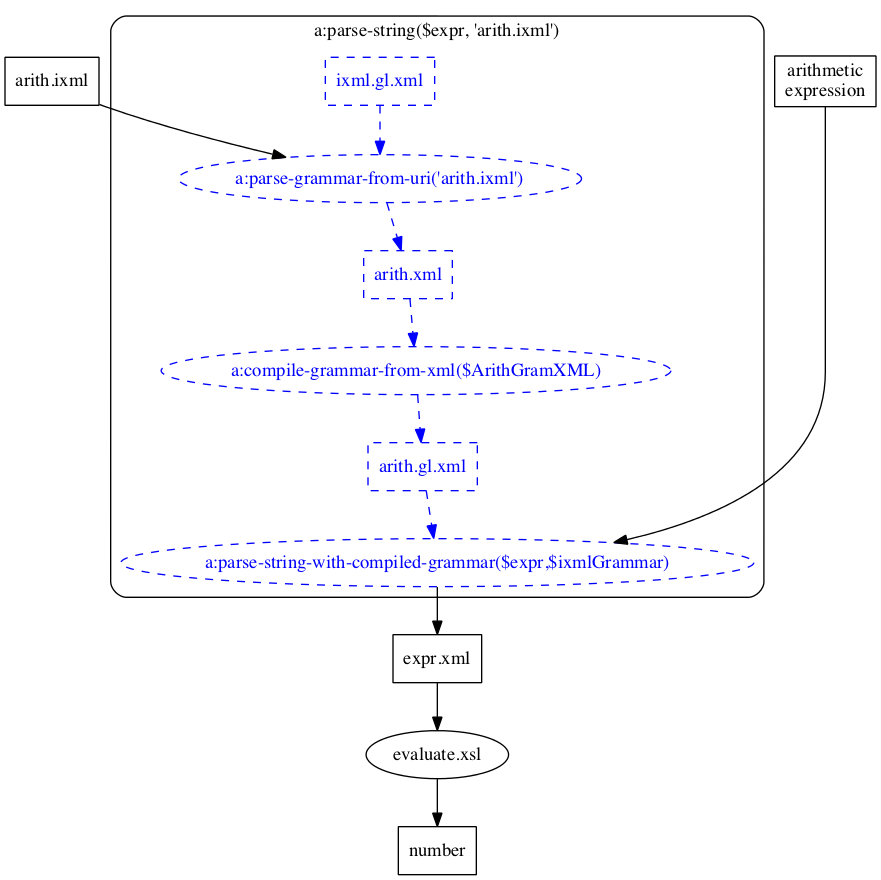
Since the grammar does not change between calls to the demo application, there is no advantage in parsing it each time and preparing it for use. Instead, the XML version is generated and prepared for use once as part of application development, and the core module of the application uses that prepared grammar rather than the original ixml form:[5]
declare variable $expression as xs:string external;
import namespace a = "http://blackmesatech.com/2019/iXML/Aparecium";
a:parse-string-with-compiled-grammar(
$expression,
"http://blackmesatech.com/2019/demos/arith/arith.gl.xml"
)
A real
application will of course
insert as many sanity checks on the input and recover
from as many user errors as possible here; the demo
application does not currently do any error checking.
If the design of the interface has been successful, the
reader will now be thinking something like That's all there
is to it?
And, as far as making the non-XML input
available as XML is concerned, yes, that is all there is
to it. It will sometimes happen that providing the
grammar needed to describe the non-XML resource will be
non-trivial[6] but one goal of
Aparecium is that once such a grammar is available, actually
gaining access to non-XML resources that follow that grammar
should be as easy as a call to the doc()
function.
The library
The preceding sections have reviewed some background information and given a simple example of the library use. We turn in this section to a discussion of the library itself: its interfaces, its current state of development, and some technical issues which arise in its development.
Basic interfaces
The implementation of Aparecium is spread across several
modules; all public-facing functions are gathered into one
module, so only one import instruction should
be needed. The functions which need the least explanation
have already been mentioned:
-
aparecium:parse-string($Input, $Grammar)takes two strings as arguments: one is the input to be parsed, the second is the ixml grammar to be used.First the grammar is itself parsed against the ixml grammar for ixml grammars to produce XML, and then the XML is annotated. To be more specific: the elements representing symbols on the right-hand side of rules are given additional attributes which all the rule to be interpreted as a Gluschkov automaton, following the algorithm given by Brüggemann-Klein 1993a. The annotated grammar is then used to parse the input, and the resulting XML document is returned.
-
aparecium:parse-resource($Resource, $Grammar)takes two URIs as arguments. The first is the URI of the input to be parsed, the second is that of the ixml grammar to be used.Each is dereferenced into a string (using the
unparsed-text()function); from this point on the course of events is as described forparse-string().
The workhorse function of the library requires that the grammar be provided neither as a URI nor as a string, but already pre-processed into annotated XML:
-
aparecium:parse-string-with-compiled-grammar($Input, $Grammar)takes a string representing the input and an annotated XML form of the grammar. It calls the Earley parser with these as arguments and returns the resulting XML document.In the simple case, the resulting XML document will be a parse tree for the input as specified in the ixml grammar: terminal symbols will all be included by default, but may be omitted from the tree if marked with a minus sign. Non-terminal symbols will by default be represented as elements, but if marked
they will be elided (though their children will continue to appear). If marked with-
, a non-terminal will become an attribute on the nearest ancestor node in the parse tree that becomes an element; this will normally be the parent, but it may be a grandparent or other ancestor if the parent and other intervening ancestors are elided. This is all as described in Pemberton 2013. (Note: in the current implementation the parse function returns a full parse tree and a separate process is needed to perform the elisions and conversions from element to to attribute.)@If the input does not parse against the grammar, an XML document with trace and diagnostic information is returned. (In the current implementation, this essentially dumps all the relevant data structures, in a way that the intended users of the library will not find helpful; it is hoped that future revisions of the library will produce better diagnostics.)
If the input is ambiguous, multiple trees are returned; this topic is discussed further below (section “Treatment of ambiguity”).
Aparecium also provides a function for fetching resources
whose publishers provide access to them with the MIME type
application/invisible-xml and a pointer to an
appropriate ixml grammar, as described in Pemberton 2013.
-
aparecium:doc($Resource)takes a string containing the URI of an invisible-XML resource, retrieves it, checks the HTTP header of the response for a pointer to the ixml grammar, retrieves and parses the grammar, and then parses the resource against the grammar and returns the resulting XML.Note: this function is not yet implemented (though it should be by the time of Balisage 2019); testing it will require configuring an HTTP server to behave as required by Pemberton 2013.
Several functions are also available for preparing grammars.
-
aparecium:parse-grammar-from-string($Grammar)takes a string containing an ixml grammar, parses it against the ixml grammar for ixml grammars, and returns the resulting XML. -
aparecium:parse-grammar-from-uri($Grammar)takes a string containing the URI of an ixml grammar, fetches the grammar by dereferencing the URI, parses it against the ixml grammar for ixml grammars, and returns the resulting XML. -
aparecium:compile-grammar-from-string($Grammar)takes a string containing an ixml grammar, parses the grammar,compiles
(annotates) it as described above, and returns the resulting annotated XML. -
aparecium:compile-grammar-from-uri($Grammar)takes a string containing the URI of an ixml grammar, fetches the grammar by dereferencing the URI, and then proceeds as for compiling from a string. -
aparecium:compile-grammar-from-xml($Grammar)takes as input the XML representation of an ixml grammar, annotates it as described above, and returns the annotated XML.
Current state of implementation
The current implementation of Aparecium is probably best described as a proof of concept. The parsing functions work (on at least some inputs) and produce XML which does represent the abstract syntax tree specified in the relevant ixml grammar. The results are satisfactory enough to allow simple demo applications like the arithmetic-expression parse described above to be built.
On the other hand, a great deal of work remains to be done before the library reaches production quality. The current test suite contains 75 or so grammars, including some chosen to exhibit odd or pathological behavior like the infinite ambiguity described below, but many more are needed. The set of available unit tests also needs to be expanded greatly. Better diagnostics are needed for cases where things go wrong. And the code needs to be improved so that things go wrong less frequently.
Currently, the implementation is written only in XQuery; it has been tested with BaseX and with Saxon, but it has not yet been tested with eXist, MarkLogic, or any other XQuery processor.
The biggest single shortcoming of the current implementation, however, is speed. This results in part from a conscious decision to worry not about speed but only about correctness, and to postpone optimization until a more complete test suite has been developed and the code is passing all the tests. The current implementation has no trouble with short inputs like those foreseen in the arithmetic-expression demo, but parse times for larger documents, even ones of only a few hundred bytes, are painfully slow, measured in minutes rather than in seconds. Fortunately, there are a number of fairly obvious ways to improve performance, and the current code is as far as possible written to hide low-level details of data representation from the high-level functions that perform parsing.
Data structures: representation of Earley items
The central data structure of the Earley algorithm is the
Earley item
: a triple (x,
y, L), where
-
x is a number between 0 and the length of the input, inclusive (the start position)
-
y is a number between x and the length of the input, inclusive (the end position)
-
L is a location in a rule of the grammar
In grammars written in Backus/Naur Form, each grammar rule consists of a single non-terminal symbol on the left-hand side and a sequence of symbols on the right-hand side. If the rules of the grammar are numbered, therefore, each Earley item can be represented by a tuple of four integers (x, y, r, i) giving the start position, end position, rule number, and index into the rule.
In regular-right-part grammars like those of invisible XML, the right-hand side of a rule is not a flat sequence of symbols but a regular expression whose basic symbols are symbols in the vocabulary of the grammar. It is possible in principle to translate a grammar from regular-right-part notation to the simpler structures of BNF-style grammars, and the translation could remain in ixml notation. But it seemed easier (as well as more fun) to make the Earley algorithm work directly with regular-right-part grammars, following the discussion in Sperberg-McQueen 2017.
The most convenient way to package together the bits of
disparate information that constitute an Earley item is (or so
it seemed to the implementor) to represent each Earley item as
an XML element of type item, with
from and to attributes
giving the start and end points. The location information is
given by including a rule element as the
only child of the item, and giving the location within the rule
in an attribute named ri (rule
index
). This in turn means that we need a way to denote
positions within a rule; a brief digression on the
representation of grammar rules in Aparecium appears to be
necessary.
In the XML notation prescribed for ixml grammars, the first rule of the arithmetic grammar given above looks something like this:[7]
<rule name="expression">
<def>
<alt>
<nonterminal name="term"/>
<repeat0>
<def>
<alt>
<nonterminal name="s"/>
<nonterminal name="addop"/>
<nonterminal name="s"/>
<nonterminal name="term"/>
</alt>
</def>
</repeat0>
</alt>
</def>
</rule>
The XML element structure of the def element corresponds in a straightforward way to the structure of the regular expression on the right-hand side of the ixml rule, which was, it may be recalled:
expression: term, (s, addop, s, term)*.
The def element and each of its descendants
represents an expression, and like all regular expressions,
these may be interpreted as defining regular languages.
The usual way to determine whether a given sequence of
symbols is in the language so defined is to translate
the regular expression into a finite state automaton (FSA).
One common way of doing so is the Thompson
construction
(Thompson 1968),
descriptions of which are readily and widely available. But
the Thompson construction involves first creating an FSA
with a potentially large number of states and
epsilon-transitions (transitions that move from one state of
the automaton to another without consuming any tokens of the
input) and then performing a tedious and expensive process
to eliminate the epsilon transitions again and reduce the
number of states. The relation between the resulting FSA
and the original regular expression is typically
obscure.
For our purposes, a better algorithm is that given by
Brüggemann-Klein 1993a, which constructs the
Gluschkov automaton
for the regular
expression (so called for the Russian mathematician Viktor
Gluschkov, whose work Brüggemann-Klein extends). I will not
attempt to describe the algorithm here, but limit myself to
a few observations. In the Gluschkov automaton, each state
corresponds one-to-one with (or just: is) one
of the basic symbols in the original regular expression[8]; the automaton also has an additional
start state which corresponds to no symbol in the
expression. In the Gluschkov automaton, we move to a given
state s whenever we read in the input a
symbol matching the symbol associated with s.
The relation between the regular expression and the
automaton is thus very simple and straightforward, and the
number of states in the FSA is predictable from the regular
expression.
To simplify description and calculation of the automaton, it is convenient if each state (and each subexpression) has a name. So the first modification we make to the representation of the rule is to add an identifier for each state. With identifiers added, the rule for expression looks something like this:
<rule name="expression">
<def xml:id="exp_def_1">
<alt xml:id="exp_alt_1">
<nonterminal name="term" xml:id="term_1"/>
<repeat0 xml:id="exp_repeat0_1">
<def xml:id="exp_def_1" nullable="false">
<alt xml:id="exp_alt_1" nullable="false">
<nonterminal name="s" xml:id="s_1"/>
<nonterminal name="addop" xml:id="addop_1"/>
<nonterminal name="s" xml:id="s_2"/>
<nonterminal name="term" xml:id="term_2"/>
</alt>
</def>
</repeat0>
</alt>
</def>
</rule>
Following Brüggemann-Klein's algorithm, we then calculate for each sub-expression (down to and including the basic symbols themselves, here all nonterminal elements) a number of properties:
-
The set of states which can be visited first in paths across the expression.
-
The set of states which can be visited last.
-
Whether the expression matches the empty string (if so, the expression is nullable).
-
For each symbol in the subexpression, what other symbols in the subexpression can follow it in a path: the follow set for the symbol.
follow:term_1 = "s_1" on the outermost
def element means that within that
expression, state s_1 can follow state term_1.
The process of calculating the values for these properties
and assigning the appropriate attributes has been referred to
elsewhere as compiling
or
annotating
the grammar. The fully annotated rule
now looks something like this:
<rule name="expression"
xmlns:follow =
"http://blackmesatech.com/2016/nss/ixml-gluschkov-automata-followset">
<def xml:id="exp_def_1"
nullable="false"
first="term_1" last="term_1 term_2"
follow:term_1=" s_1"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<alt xml:id="exp_alt_1"
nullable="false"
first="term_1" last="term_1 term_2"
follow:term_1=" s_1"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<nonterminal name="term" xml:id="term_1"
nullable="false"
first="term_1" last="term_1"
follow:term_1=""/>
<repeat0 xml:id="exp_repeat0_1"
nullable="true" first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<def xml:id="exp_def_1"
nullable="false" first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="">
<alt xml:id="exp_alt_1"
nullable="false" first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="">
<nonterminal name="s" xml:id="s_1"
nullable="false"
first="s_1" last="s_1"
follow:s_1=""/>
<nonterminal name="addop" xml:id="addop_1"
nullable="false"
first="addop_1"
last="addop_1"
follow:addop_1=""/>
<nonterminal name="s" xml:id="s_2"
nullable="false"
first="s_2" last="s_2"
follow:s_2=""/>
<nonterminal name="term" xml:id="term_2"
nullable="false"
first="term_2"
last="term_2"
follow:term_2=""/>
</alt>
</def>
</repeat0>
</alt>
</def>
</rule>
The finite state automaton whose states are the basic
symbols of the expression rule (plus an
extra start state) and whose transitions and other properties
are given by the attributes first,
last, and follow:*
attributes on the outermost def element can
be illustrated by the following diagram:
Figure 6
Our digression into the structure of rules is almost complete. It remains only to be observed that the current state of an FSA which has partially recognized a string is given fully by the name (the identity, really) of the state. (That is pretty much a defining feature of a finite state automaton: its future behavior is defined solely by the identity of the current state.)
So we can represent the current position in the right-hand side of a rule by recording the name of the current state: that is, given the way the Gluschkov automaton is constructed, the identifier assigned in the rule to the corresponding terminal or non-terminal symbol. If nothing has yet been read, we are in the start state for the rule. By convention, the start state of any rule is named q0.
This concludes the digression onto the structure of grammar rules in Aparecium.
We can now show an example of an Earley item as
represented in the current implementation. At position 20 in
the string
(that is, just after the right parenthesis), the parsing
algorithm will generate an Earley item that means, in effect,
23 + 1834 / (60 - 3) - 9after reading the input string from position 0 to
position 20, the FSA for rule expression is
in state term_2.
That Earley item
will have the following form:
<item from="0" to="20" ri="term_2">
<rule name="expression"
xmlns:follow="http://blackmesatech.com/2016/nss/ixml-gluschkov-automata-followset">
<def xml:id="exp_def_1"
nullable="false"
first="term_1" last="term_1 term_2"
follow:term_1=" s_1"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<alt xml:id="exp_alt_1"
nullable="false"
first="term_1" last="term_1 term_2"
follow:term_1=" s_1"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<nonterminal name="term" xml:id="term_1"
nullable="false"
first="term_1" last="term_1"
follow:term_1=""/>
<repeat0 xml:id="exp_repeat0_1"
nullable="true"
first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="s_1">
<def xml:id="exp_def_1"
nullable="false"
first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="">
<alt xml:id="exp_alt_1"
nullable="false"
first="s_1" last="term_2"
follow:s_1=" addop_1"
follow:addop_1=" s_2"
follow:s_2=" term_2"
follow:term_2="">
<nonterminal name="s" xml:id="s_1"
nullable="false"
first="s_1" last="s_1"
follow:s_1=""/>
<nonterminal name="addop" xml:id="addop_1"
nullable="false"
first="addop_1"
last="addop_1"
follow:addop_1=""/>
<nonterminal name="s" xml:id="s_2"
nullable="false"
first="s_2" last="s_2"
follow:s_2=""/>
<nonterminal name="term" xml:id="term_2"
nullable="false"
first="term_2"
last="term_2"
follow:term_2=""/>
</alt>
</def>
</repeat0>
</alt>
</def>
</rule>
</item>
This representation is convenient for the programmer but has a practical flaw. There will be at least one Earley item for each terminal symbol in the input; in ixml grammars, that means one for each character. Making the rule element a child of the item element makes it extremely convenient to consult the rule when needed, but it also requires that the XQuery or XSLT implementation make a new copy of the rule for each Earley item created (because each copy of the rule will have a different parent element). The frequent copying creates a perceptible strain on memory in the current implementation of Aparecium. A simpler representation of the Earley item would not reproduce the rule but merely point at it, thus:
<item from="0" to="20" rulename="expression" ri="term_2"/>
Better performance can also come from representing the Earley
item not as an element but as a map which points at, rather than
naming, the rule and state (assuming that the variables
$rule and $state have
been appropriately initialized:
map {
"from": 0,
"to": 20,
"rule": $rule,
"ri": $state
}
Changing the representation of items to use maps instead of
elements reduced parse time for grammars in the test suite
between 15% and 30%. This was much less than had been
expected. A much more dramatic effect (seven-fold speedup)
came from changing the representation of the set of Earley
items being calculated by the algorithm to make the search
for Earley items with specific properties faster.
Treatment of ambiguity
A sentence is ambiguous if it has more than one derivation that follows the rules of the grammar. One of the great advantages of Earley parsing is that it is robust in the presence of ambiguity: if there is exactly one derivation of a sentence, the Earley parser will find it; if there is more than one, the Earley parser will find more than one. This contrasts sharply with most widely used parsing techniques, which cannot function if the grammar has any ambiguous sentences. Unfortunately, existing parsing tools are often not much help detecting ambiguity or helping the grammar author remove it. So a great deal of time can be spent, with tools like yacc, trying more or less random changes to the grammar in an attempt to eliminate the parsing conflicts detected by the tool.
For ambiguous sentences, Pemberton 2013 prescribes that an ixml parse should return any one of the parse trees, with a flag to signal that there are other parse trees for the input. This is clearly satisfactory if it is known that any ambiguity is inconsequential. If a grammar for arithmetic expressions is ambiguous only because whitespace may be regarded either as a child of a term or as the child or an expression, then it does not matter for numerical evaluation which tree is selected: whitespace plays no role. The rule may be less satisfactory, however, if the two parses would assign different meanings to the sentence. In such a case, it may be useful for a grammar writer (though perhaps not a grammar user) to be able to compare the two parses; that comparison may help make the source of the ambiguity clear.
For this reason, the current version of Aparecium deviates from the rule enunciated by Pemberton: for ambiguous sentences Aparecium returns multiple parse trees. In some simple cases, it returns all parse trees, but that is not and cannot be true in general: in some cases, a sentence may have an infinite number of parse trees.
Consider the following grammar:
A: A; "a".
An A consists either of another
A or of the letter a. The only sentence in the language defined by this grammar is
a, but it has an infinite number of parse trees. XML representations of a few of these include:
<A>a</A>
<A><A>a</A></A>
<A><A><A>a</A></A></A>
...
Another small grammar illustrates a different kind of infinity in parse trees:
S: (X)*. X: "x"; {nil}.
Here the language consists of strings of zero or more
occurrences of x, but each sentence has an infinite number of parse trees. For the sentence
x, the parse trees include the following.
<X>x</X>
<X><X/>x</X>
<X>x<X/></X>
<X><X/><X/>x</X>
<X><X/>x<X/></X>
<X>x<X/><X/></X>
...
In both of these cases, Aparecium will detect the infinite ambiguity and return only a finite number of parse trees.
Future work
The immmediate task for the ongoing work on the library is to change it from a proof of concept to a reliable practical tool for use by XQuery and XSLT programmars. A systematic suite of unit tests and system tests is important both to help establish correctness of the code and to help ensure that ensuing attempts to improve performance do not introduce incorrect behavior.
When complete (or less incomplete), the library will be released under an open-source license; dual licensing may be available for those who require other terms.
Performance improvements are necessary before the library can be a useful tool for more than specialized applications and short inputs. The obvious place to start is with the representation of Earley items. Reducing the amount of copying that need be done, and the amount of memory needed, as the set of items grows, may make a signficant difference. Improving the processor's ability to find the needed Earley item in a search of the current set is also desirable. Earley's original algorithm is built around a data structure in which items are in effect indexed by their start value; it seems straightforward to do the same using maps in XQuery and XSLT 3.0.
Performance comparisons with other available tools will also be of interest. It is to be expected that Earley parsing will often be slower than parsing using other techniques[9]; it will be interesting to see how much slower it is.
Some additional features seem potentially desirable. On
the assumption that many users will want to parse non-XML
resources conforming to some widely known notations like CSS,
JSON, XPath, or XPointer, it might be helpful to package
grammars for such notations with the library. That in turn
would make it possible to let the aparecium:doc()
function select an ixml grammar based on the MIME type of the
resource, even if the publisher has not provided a grammar.
Since many published notations are designed to be parseable
with existing parser tools, it might also be feasible to
package parsing functions for some notations with the libary,
and use a faster algorithm when possible. This suggests
outfitting Aparecium with a pre-populated repository of
grammars and parsers and providing methods to allow the user
to add and delete items from the repository.
In a related vein, it would be desirable to have a library of functions for the analysis of grammars. Given an ixml grammar, such a library could determine whether the grammar as given is LL(1) or LR(1) and thus suitable for parsing with other tools. It would also be desirable to be able to test grammars for ambiguity. This is not, in general, a soluble problem: there is no algorithm for detecting ambiguity that will work in all cases. But there are methods which will detect at least some ambiguities, and which can explain and illustrate the ambiguity usefully. Utilities for translating grammars between notations might also be useful, although few grammatical notations have free-standing specifications in the style of ixml: many are tied to specific pieces of software and have documentation which is at best imperfect.
I hope to have shown in this paper that invisible XML can be made useful to XSLT and XQuery programmers, independent of the willingness of information publishers to provide invisible XML grammars for their information, by providing a library that allows them to supply the grammars themselves. Using non-XML resources for which an invisible XML grammar is available thus becomes as simple as using XML resources: a call to a single function, to load the resource as an XML document. The current implementation of Aparecium provides a demonstration that such a library can exist; what is needed next is work to move it from a proof of concept to a useful tool.
References
[Beckerle / Hanson 2014] Beckerle, Michael J., and Stephen M. Hanson. Data Format Description Language (DFDL) v1.0 Specification. Open Grid Forum DFDL Working Group, Document GFD-P-R.207, September 2014. On the Web at https://www.ogf.org/documents/GFD.207.pdf
[Brüggemann-Klein 1993a]
Brüggemann-Klein, Anne.
1993.
Regular expressions into finite automata
.
Theoretical Computer Science
120.2 (1993): 197-213. doi:https://doi.org/10.1016/0304-3975(93)90287-4.
[Brüggemann-Klein/Wood 1998]
Brüggemann-Klein, Anne,
and
Derick Wood.
1998.
One-unambiguous regular languages
.
Information and computation
140 (1998): 229-253. doi:https://doi.org/10.1006/inco.1997.2688.
[ETJ 2018] Ed J (ETJ). XML::Invisible. Perl module. Version 0.04, 18 October 2018. On the Web at https://metacpan.org/pod/XML::Invisible
[Grune/Jacobs 2008] Grune, Dick, and Ceriel J. H. Jacobs. 2008. Parsing techniques: a practical guide. Second edition [New York]: Springer, 2008.
[Kegler 2018] Kegler, Jeffrey. Marpa::R2. Perl module. Version 8.000000, 17 December 2018. On the Web at https://metacpan.org/pod/Marpa::R2
[Krupnikov 2003]
Krupnikov, Ari.
STnG — a Streaming Transformations and Glue framework
.
Paper given at Extreme Markup Languages 2003,
Montréal, sponsored by IDEAlliance.
On the Web at http://conferences.idealliance.org/extreme/html/2003/Krupnikov01
/EML2003Krupnikov01.html
[Lavinio 2007]
Lavinio, Tony.
Using XQuery and XSLT on NonXML
Data
.
Paper presented at XML 2007.
Slides on the web at https://www.powershow.com/view/3c581-YjlmM/Using_XQuery_and_XSLT_on_NonXML_Data_powerpoint_ppt_presentation
[Novatchev 2003]
Novatchev, Dimitre.
Functional programming in XSLT
using the FXSL library
.
Paper given at Extreme Markup Languages 2003,
Montréal, sponsored by IDEAlliance.
On the web at http://conferences.idealliance.org/extreme/html/2003/Novatchev01/EML2003Novatchev01.html
[Novatchev 2006a]
Novatchev, Dimitre.
Higher-Order Functional Programming
with XSLT 2.0 and FXSL
.
Paper given at Extreme Markup Languages 2006,
Montréal, sponsored by IDEAlliance.
On the web at http://conferences.idealliance.org/extreme/html/2006/Novatchev01/EML2006Novatchev01.html
[Novatchev 2006b] Novatchev, Dimitre. FXSL -- the Functional Programming Library for XSLT. Sourceforge site at http://fxsl.sourceforge.net.
[Pemberton 2013]
Pemberton, Steven.
Invisible XML
.
Presented at Balisage: The Markup Conference 2013,
Montréal, Canada, August 6 - 9, 2013.
In
Proceedings of Balisage: The Markup Conference 2013.
Balisage Series on Markup Technologies, vol. 10 (2013).
doi:https://doi.org/10.4242/BalisageVol10.Pemberton01.
[Pemberton 2018]
Pemberton, Steven.
Invisible XML
[web page].
Last modified 16 September 2018.
On the Web at https://homepages.cwi.nl/~steven/ixml/.
[Pemberton 2019a]
Pemberton, Steven.
Invisible XML Specification (Draft)
.
Version: 2019-01-28.
On the Web at https://homepages.cwi.nl/~steven/ixml/ixml-specification.html.
[Pemberton 2019b] Pemberton, Steven. [Home page.] Last modified 9 April 2019. On the Web at https://homepages.cwi.nl/~steven/.
[Rose 2005]
Rose, Kristoffer H.
Introducing the Data Format Description Language
.
Paper given at Extreme Markup Languages 2005,
Montréal, sponsored by IDEAlliance.
[Sperberg-McQueen 2013]
Sperberg-McQueen, C. M.
Recursive descent parsing
in XQuery (and other functional languages)
.
Blog post, 7 January 2013.
On the web at http://cmsmcq.com/mib/?p=1260.
[Sperberg-McQueen 2017]
Sperberg-McQueen, C. M.
Translating imperative algorithms
into declarative, functional terms:
towards Earley parsing in XSLT and XQuery
.
Presented at Balisage: The Markup Conference 2017,
Washington, DC, August 1 - 4, 2017.
In Proceedings of Balisage: The Markup Conference 2017.
Balisage Series on Markup Technologies, vol. 19 (2017).
doi:https://doi.org/10.4242/BalisageVol19.Sperberg-McQueen01.
[St. Laurent 2001]
St. Laurent, Simon.
Regular fragmentations:
Treating complex textual content as markup
.
Paper given at Extreme Markup Languages 2001,
Montréal, sponsored by IDEAlliance.
On the Web at http://conferences.idealliance.org/extreme/html/2001/StLaurent01/EML2001StLaurent01.html
[Thompson 1968]
Thompson, Ken.
Regular expression search algorithm
.
CACM
11.6 (1968): 419-422. doi:https://doi.org/10.1145/363347.363387.
[Zhu 2005] Zhu, Yi. Implementing a subset of DFDL: A basic parser for a subset of the DFDL specification and related libraries. MSc thesis, Univ. of Edinburgh, 2005. On the Web at https://static.epcc.ed.ac.uk/dissertations/hpc-msc/2004-2005/0764527-9j-dissertation1.2.pdf
[1] The proposition that deep nesting can make processing simpler is one of a number of important insights into markup which Lynn Price worked for a long time to get into my head. She often gave it as a motivation for the presence in SGML of markup minimization features like OMITTAG, SHORTREF, and DATATAG: in the ideal case, they provide a notation simple enough to be suitable for human authoring and rich enough to make processing easier.
[2]
In many cases, a grammar can be reworked to become LL(1), or
LR(1), or whatever is required. Unfortunately, there is no
simple set of rules (and in fact no reliable set of rules at
all) to say what changes we can make in a grammar without
changing the language recognized by the grammar. If there
were such rules, the tool could do the transformation for us.
Intuitively, experience with existing parser-generation tools
leads many users to believe that any reasonable
language can be defined by a grammar satisfying the
constraints of the tool, and that languages which persist in
being unreasonable can usefully be improved
by
modifying them until they become reasonable again. This
belief may have some truth to it, although at first glance it
looks as if the parsing tool were merely training its users
not to want what it cannot provide.
[3]
Among those best known are the Cocke / Younger / Kasami (CYK)
algorithm, the Earley algorithm, and a number of
generalized
algorithms (generalized LR,
generalized LL, generalized LC) and backtracking algorithms.
By far the best source for descriptions of these and other
parsing algorithms is Grune/Jacobs 2008.
[4]
Just as parse-resource() takes two URIs for the
input and the grammar as arguments, so
parse-string() takes two strings. It is thus
necessary to dereference the URI for the grammar, as shown in
the example.
[5]
The gl in the filename
arith.gl.xml reflects the fact that (as is
about to be explained below) this version of the grammar has
annotations that allow it to be interpreted as a set of
Gluschkov automata
.
[6] As a case in point: the arithmetic grammar shown is not the first draft; several errors have needed to be fixed, and the version shown here still has a potentially painful problem in the handling of whitespace characters. Grammar development is not very hard, but it can raise some tricky issues. Whitespace handling is consistently one of them. SGML users may remember nostalgically the observation known as Goldfarb's Law: if a text processing application has bugs, at least one of them will have to do with whitespace handling. Grammar development appears to be subject to this law.
[7] The syntax shown is that currently used by Aparecium; it is based on the grammar exhibited in Pemberton 2013 and on a 2016 revision of the grammar. In the current version of the ixml specification (Pemberton 2019a) the structure for this rule is the same, but the def element has been renamed alts. Other changes in the syntax are not visible in this example.
[8] Formally, a finite state automaton has a set
of states, but it is immaterial what the states actually
are: the only intrinsic property they need to possess is
that they must be distinguishable from each other, which is
implicit in the phrase set of states
: if we cannot
distinguish the elements of a set from each other, then we
cannot handled it as a set after all.
It follows from this that there is
no necessity to imagine a set of states that correspond 1:1
to the symbols of the regular expression; we can take the
set of symbols (symbol tokens, to be exact) in the
expression, and make that be the set of states in our
automaton.
[9] Grune and Jacobs say (p. 547 of Grune/Jacobs 2008)
It should be noted that if any of the general parsers
performs in linear time, it may still be a factor of ten or so
slower than a deterministic method, due to the much heavier
administration they need.