Introduction
A schema for XML expresses constraints for those XML documents that conform to the schema, the schema's instances. XML Schema as a language expresses so-called XSD schemas. This paper is concerned with the part of XML Schema that expresses structural constraints [GST2012] as opposed to data value constraints.
Four basic patterns have been identified in the literature how a schema can be built [C2006b, M2002, P2015]. The criteria for the four patterns are whether the type definitions or the element declarations in the schema are all global or all local. The names of the four patterns are Salami Slice (all global element declarations, all local type definitions), Russian Doll (all local element declarations, all local type definitions), Venetian Blind (all local element declarations, all global type definitions) and Garden of Eden (all global element declarations, all global type definitions).
Current literature defines these patterns and discusses their properties, for example in terms of re-use, encapsulation, coupling and cohesion [C2006b, M2002, P2015]. In this paper, we discuss the expressive power of the four patterns: which pattern can or cannot be rewritten into which other pattern while maintaining the set of instances. It turns out that Venetian Blind is the most powerful pattern. Any XSD schema, even those that do not follow any of the four patterns strictly, can be rewritten into the Venetian Blind pattern. The two patterns Salami Slice and Garden of Eden are equivalent in descriptional power. These are the only transformations that can be done completely, for any schema that adheres to the source pattern, and they can be done algorithmically. Hence, Venetian Blind is strictly more powerful than any of the three other patterns and Russian Doll is incomparable to Salami Slice and to Garden of Eden. These results are summarized in Figure 11
A unique contribution of this work is that it is based on explicit models for schemas and documents and on their relationships and properties. This enables us to delimit the area of discourse and to state results as theorems that have rigorous proofs. In addition, we illustrate definitions, phenomena and operations with concrete examples in XML Schema syntax.
This paper is organized as follows:
-
Informal definition of an XSD schema and the four patterns by example.
-
Formal model of an XSD schema and its instances. Their properties and operations.
-
Formal definition of the four patterns and the ways in which their expressive powers can be compared.
-
Comparing the expressive power of the four patterns.
-
Local into global for type definitions.
-
Local into global for element declarations.
-
Limitations of the Russian Doll schema.
-
From global to local
-
We conclude the paper with a number of discussion points and some final remarks.
The four patterns for XSD schemas in XML Schema syntax
An XSD schema contains type definitions and element declarations.
We only consider a sub-class of so-called complex type definitions which, ignoring attributes, define how an XML element that conforms to the type must be structured: what sequences of sub-elements can it have and which type constraints apply to each of the elements in a sequence. Such a definition uses some kind of regular expression formalism and is called a content model. Hence, a content model describes sequences of elements and associates a type definition with each element within a sequence. Using the definition below, we can also say that a content model describes sequences of element declarations.
Type definitions and content models in XML Schema also constrain text content and data types of XML elements. In this work, the model of XML documents allows for text content. The model of XML schemas does not define any kind of constraints for text content, though. We will see the implication of that decision in the definition of validity below.
An element declaration associates an element name with a type definition.
The type definitions and element declarations that are directly contained in an XSD schema, at its outer-most level, are called global. In XML Schema, global type definitions are identified by a name; global element declarations are identified by the element name that is part of the element declaration. Names of global type definitions and names of globally declared elements form their own namespaces and must be unique within these namespaces.
A content model in a type definition declares elements that occur in sequences. These declarations can be local to the content model, or they can be references to global element declarations. Such references are by element name.
Analogously, an element declaration, be it global or local, has a type definition that can be local to the element declaration or a reference to a global element declaration. Such references are by name of the type definition.
A local element declaration has by definition a name. Local type definitions are anonymous.
Figure 1 has an example of a mixed XSD schema that has both local and global element declarations and type definitions; see [V2002] for the Peanuts tradition in schemas.
Figure 1: An XSD schema of mixed type This XSD schema has global element declarations for
Formally, the type definitions for book, title and author, of which
title and author are referenced from within
the schema through the element xs:element with attribute
ref. There are also local element declarations, for example
one for character. The schema has one global type definition
for bookType, which is referenced in the element declaration
for book. There is also a local type definition for element
character.name,
friend-of, since and
qualification are references to a globally defined data
type, namely xs:string. We discount these references when we
define the four types, since they do not concern element structure. They are
on a par with mixed-content indicators in content models, which we also
ignore.
Global element declarations and type definitions can be re-used within an XSD schema and also between different XSD schemas. Local element declarations and type definitions are encapsulated within the type definitions and element declarations to which they belong. They are only visible within these parent constructs and cannot be re-used. Hence, XML Schema gives schema designers the flexibility to satisfy specific requirements of re-use and encapsulation when designing an XSD schema.
Four pure patterns have been identified in the literature how a schema can be built [C2006b, M2002, P2015]. The criteria for the four patterns are whether the type definitions or the element declarations in the schema are all global or all local. The names of the four patterns are Salami Slice (all global element declarations, all local type definitions), Russian Doll (all local element declarations, all local type definitions), Venetian Blind (all local element declarations, all global type definitions) and Garden of Eden (all global element declarations, all global type definitions).
The only deviations in this uniformity are that schemas that follow the Russian Doll or the Venetian Blind patterns can have global element declaration, which define the root element of instances of the schema; those global element declarations cannot be referenced, though, in these patterns. In these two patterns, the entry points into an instance can be constrained. In the other two patterns, any element can be an entry point into an instance.
[TODO: explain the names of the four patterns.]
We condense the definition of the four patterns in the following table.
Figure 2: The matrix of the four patterns

We have re-written the mixed schema in Figure 1 into each of
the four patterns. Each of these four schemas validates the two documents
book and character below. Please be aware that these
transformations were possible because the locally declared elements in the original
mixed schema have unique names.
[TODO check for uniform font sizes in the examples (the screens from which the screen shots are made should have identical widths). The same should hold true for the width of the selection window when making the screenshot. Alternatively, how can we include formatted code directly?]
Figure 3: The XML document book

Figure 4: The XML document character

Figure 5: A Russian Doll schema with instances book and
character

Figure 6: A Salami Slice schema with instances book and
character

Figure 7: A Venetian Blind schema with instances book and
character

Figure 8: A Garden of Eden schema with instances book and
character

Formally, we have defined the four patterns only for XSD schemas. There is, however, a natural transformation from an XML DTD into an XSD schema, which results in a Salami Slice pattern. [TODO: describe the transformation, reference literature or behaviour of tools such as oXygen]
Modeling XML documents and XSD schemas
The model for XML documents and its properties
The XQuery and XPath Data Model XDM [WSC2017] defines an XML document [BPS2008] as a number of interrelated components that are called nodes (or information items in other contexts). In the context of this discussion, we only consider two types of nodes, namely element nodes and text nodes. An element node has a name and consists of a sequence of child nodes, which can be element nodes or text nodes. A text node has a sequence of Unicode characters as its value.
The consists-of relationship between an element node and any of its children nodes needs to form a single finite ordered tree structure. The unique root of such a tree structure is called an XML document.
We assign a finite depth to each element node,
starting with depth 0 for the root node. We define the height of an XML document as the maximal depth of any of the element
nodes that it contains. The XML document book that we have defined
above has height 2; the XML document character that we have
defined above has height 1. Please be aware that height and depth only take
element nodes into account, not text nodes.
We provide an UML diagram for the components of an XML document which incidentally follows the composite pattern.
Figure 9: Modeling components of an XML document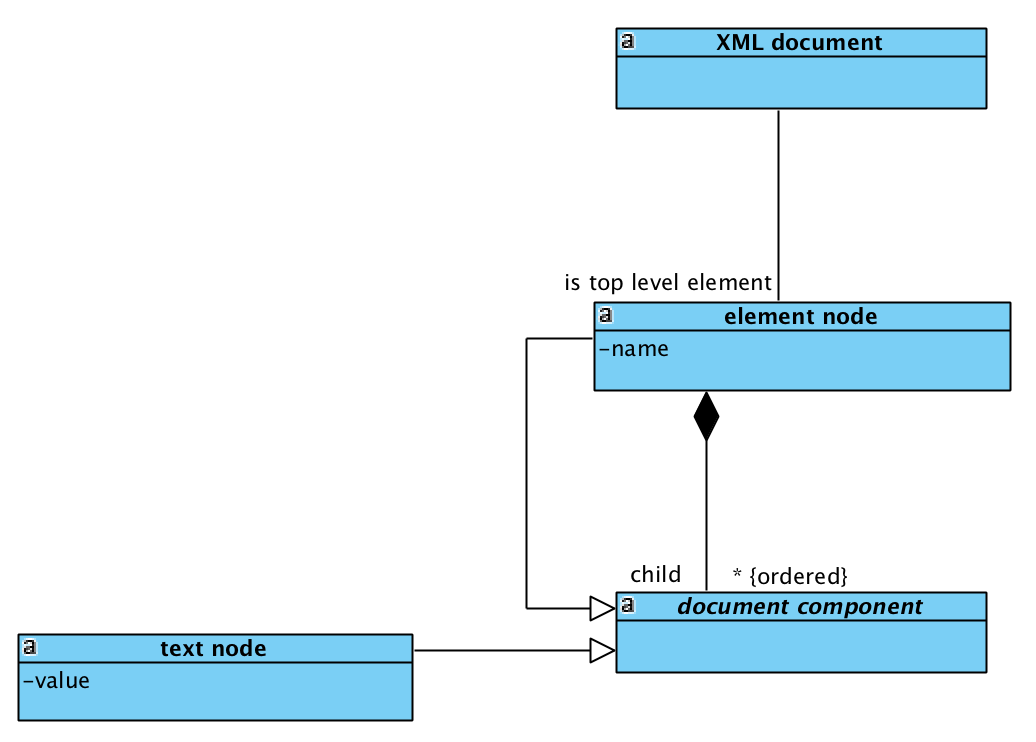
The model for XML schema and its properties
The W3C Recommendation for XML Schema (Structures) [GST2012] defines an XSD schema on a conceptual level as a set of schema components. In the context of this discussion, we only consider two types of schema components, namely complex type definitions, which we call just type definitions, and element declarations.
In its simplest version, a type definition has an optional name and a content model. A detailed definition of content model is not necessary for this discussion. It suffices to know that a content model is some kind of expression over element declarations, each of which either is global and referenced in the content model by its name or is local (see below)[1]. The content model matches finite and ordered sequences of element declarations.
An XSD schema consists at a global level of a set of uniquely named type definitions. Unnamed type definitions can occur locally within element declarations, as we will see.
In its simplest version, an element declaration has a mandatory name and a type definition. The type definition can be global, in which case it is referenced by its name, or it can be locally defined within the element declaration, in which case it is unnamed and cannot be accessed from outside the element declaration.
In addition to named type definitions, an XSD schema can contain uniquely named element declarations at a global level. As we have mentioned, element declarations can also be defined locally within a type definition. Please remember that names in element declarations are always mandatory, even for locally defined element declarations.
Let us be clear about the consists-of relationship in an XML schema. The schema consists of global element declarations and of global type definitions. An element declaration consists of a local type definition, if there is any (it does not consist of a reference to a global type definition). A type definition has a content model that is built over a number of element declarations; the type definition consists of all the local element declarations over which its content model is built (it does not consist of any of the references to global type declarations over which its content model is built.)
The consists-of relationship of an XML schema is striped. Element declarations consist of type definitions, which are always local, and type definitions consist of element declarations, which are always local. An XML schema consists of element declarations and type definitions, which are always global.
The consists-of relationship of an XML schema needs to form a single finite unordered tree, with the schema itself as its root. All global type definitions need to be referenced from within the schema. The global element declarations serve as entry points into a schema, as declarations against which XML documents can be verified. They do not need to be referenced from within the schema.
We provide an UML diagram for the components of an XSD schema.
Figure 10: Modeling components of an XSD schema
Let us go back to the XSD schema of mixed type that we have defined above. The
schema consists of global element declarations for book,
title and author and of a global type definition for
bookType. The type definition for bookType consists of
an element declaration for character, which consists of element
declaration for name, friend-of, since und
qualification. This describes the complete consists-of relationship
of the schema. The single global type definition in the schema, the one for
bookType, is referenced in the element declaration for
book. Hence, the schema satisfies our constraints.
In analogy to XML documents, we assign a depth to each component of an XML schema in accordance to the consists-of relationship, assigning depth 0 to the schema itself, depth 1 to all its global element declarations and global type definitions and so on, following the consists-of relationship[2]. The height of an XML schema is then the maximum of all the depths of a schemas components. The height of the schema of mixed type that we have included above is 3.
Validity
We define now when an element declaration eD
matches an element node eN, or
when an element node eN is valid
with respect to an element declaration eD.
For that definition, consider the children of eN that are element
nodes. They form a potentially empty sequence
eN1,…,eNk.
Furthermore, let tD be the type definition of eD. Then,
eD matches eN when the content model of
eD matches a sequence of element declarations
eD1,…,eDk
such that (a) the names of eNi and
eDi are identical and (b) each
eDi matches
eNi, for all i between 1
and k
This is a recursive definition that is well-founded due to the structure of the consists-of relationship for document nodes. The definition disregards text nodes in documents and any provisions that a real content model in a real XML schema might make for them.
If only the clause (a) is met, then we say that the element declaration matches the element node locally.
Note that validity does not depend on the status of element declarations or type definitions as local or global.
An XSD schema matches an XML document (or an XML document is valid with respect to an XSD schema or an XML document is an instance of an XSD schema) if the XSD schema has a global element declaration that matches the XML document, which is an element node in our model.
As a corollary, an XSD schema that has no global element declaration has no instances.
The language L(s) of an XSD
schema s is the set of all its instances. Two XSD schemas are
equivalent if their languages (their sets of
instances) are equal.
Operations on schemas
In this work, we ultimately want to rewrite XML schemas from one pattern into another whereever possible while preserving their languages. These transformations are done incrementally by rewriting single type definitions or element declarations from global to local and vice versa. We discuss how these single rewrites are done and under which conditions they are possible. With the exception of turning local element declarations into global element declarations, a single rewrite that preserves schema integrity and languages is always possible. As we will see, restrictions apply when we want to iterate the single transformations.
A single reference to a global element declaration or to a global type definition can easily replaced with a local element declaration or local type definition, respectively. In the case of a type definition, if the schema has no other reference to the global type definition, the global type definition has to be removed from the schema to preserve its integrity. This operation does preserve language.
If we have a local type definition, it is contained in some element declaration and it is unnamed. We can give it a new and unique name and make it global, replacing the local type definition with a reference to the now global type definition using its new and unique name. This preserves schema integrity and language.
If we have a local element declaration, it is contained in some type definition via its content model. In contrast to local type definitions, a local element declaration already has a name. Only if this name is not used in any global element declaration of the schema can we make the element declaration global and replace the local declation in the type definition with a reference. This preserves schema integrity and language. If this name is already used in some global element declaration of the schema, we might be tempted to resolve the name conflict by giving the element a new and unique name and to proceed as above. This would, however, change language.
In summary, we have presented transformations to make a single global type definition and a single global element declaration local while preserving schema integrity and language. The same is true for making a single local type definition global. We have also pointed out why a naive approach to make even a single local element declaration global fails due to name conflicts. We will investigate later under which conditions these single transformations can be iterated with the goal of transforming from one schema pattern into another.
Defining the four patterns for XSD schemas
An XSD schema is a Russian Doll schema (or exhibits
the Russian Doll pattern) if all its element declarations and all its type definitions
are local, with the exception of global element declarations that are not referenced
in
the schema. We denote the set of all Russian Doll schemas
with RD.
An XSD schema is a Garden of Eden schema (or exhibits
the Garden of Eden pattern) if all its element declarations and all its type definitions
are global. We denote the set of all Garden of Eden schemas
with GE.
An XSD schema is a Salami Slice schema (or exhibits
the Salami Slice pattern) if all its element declarations are global and all its
type
definitions are local. We denote the set of all Salami Slice schemas
with SL.
An XSD schema is a Venetian Blind schema (or exhibits
the Venetian Blind pattern) if all its element declarations are local, with the
exception of global element declarations that are not referenced in the schema,
and all
its type definitions are global. We denote the set of all Venetian Blind schemas
with VB.
We denote the universal set of XSD schemas with U.
We refer back to Figure 1 for the pattern matrix.
In this paper, we discuss the descriptional power of these patterns. We base the
discussion on a number of constructive definitions.
That means that we not only claim the existence of certain things but that we can
compute them algorithmically. [TODO: replace ASCII graphics for arrows with Unicode
characters. The use of o for one end of the relationship is unfortunate and
is solely motivated by the line endings that are available in PowerPoint.]
-
A set of XSD schemas
S'is more powerful than a set of XSD schemasS(S ---> S') if there is an algorithm or a process that constructs for each schema inSan equivalent schema inS'. -
A set of XSD schemas
S'is incongruent with a set of XSD schemasS(S o--- S') if we can identify a specific schema inS'that is not equivalent to any schema inS. -
A set of XSD schemas
S'is strictly more powerful than a set of XSD schemasS(S o---> S') ifS'is more powerful than and incongruent withS. -
A set of XSD schemas
S'is equally powerful to a set of XSD schemasS(S <---> S') ifS'is more powerful thanSandSis more powerful thanS'. -
A set of XSD schemas
S'is incomparable to a set of XSD schemasS(S o---o S') ifS'is incongruent withSandSis incongruent withS'.
Comparing the expressive powers of the four patterns
Let us consider if or under which conditions local element and type definitions can be made global and vice versa. As we will see, if we make local constructs global, we might run into naming conflicts on the global level, and if we make global constructs local, we might run into infinite recursion.
We can summarize our results in a diagram. [TODO add a triangular diagram that better illustrates the hierarchy.]
Figure 11: Complete transformation Matrix
Local into global for type definitions
Let us first look at the question of making local constructs global, and let us
start with type definitions. The tree constraint of the consists-of relationship
implies that an XSD schema s has only a finite number of local
type definitions. As we have seen, we can transform the schema into another XSD
schema s' by making a single local type definition
of s global. This transformation has the following
properties:
-
It preserves schema constraints.
-
It preserves language; that is
L(s) = L(s'). -
It reduces the number of local type definitions by 1; that is, it introduces no new local type definitions (though it may move some existing ones into a different context).
Therefore, step by step, we can transform schema s into another
schema that has no local type definitions. Since the single-step transformation
is
constructive, then so is the complete transformation.
We now state our first theorem on expressive power.
Theorem
VB is more powerful than RD. GE is more
powerful than SS.
Figure 12: Transformation Matrix (A)
After our previous discussion, the proof is obvious: each Russian Doll schema can be transformed into a Venetian Blind schema by making its local type definitions global. The same argument holds for Salami Slice and Garden of Eden schemas.
Local into global for element declarations
We have seen that the naïve attempt to make local element declarations global fails, due to name conflicts. We can even prove that there cannot be any construction at all who achieves this.
Let us consider the language langA1 that contains just a single XML
document docA1, namely the one that is represented by
<a><a/></a>. The document docA1 has two element
nodes named a, with one being the child of the other, and is of depth 1.
Using local element declarations, we can define an XSD schema schemaA
that has a single global element declaration for an element a and
a type definition that denotes a single sequence of length 1 that consists of
a
local element declaration for an element a that is declared to be
empty. The figure below defines such a schema that exhibits the Russian Doll
pattern, and we know from the previous section that we could just as well define
it
as a Venetian Blind schema.
Figure 13: The XSD schema schemaA
We claim now that an XSD schema that declares element a only
globally cannot have docA1 as its sole instance. The point is that, if such a
schema matches docA1, then the global element declaration for a
must allow a sub-element a that has the same type definition
associated with it, as well as the empty sequence. Therefore, the documents that
are
represented by <a/> (docA0) or by
<a><a><a/></a></a> (docA2) are additional
instances of the schema, and so are all bounded chains docAi of
elements a.
We have demonstrated that the language langA1 is the language of
some Venetian Blind schema and of some Russian Doll schema, but that it cannot
be
the language of any Salami Slice or Garden of Eden schemas.
Theorem VB and RD are both incongruent with each of SS and GE
Figure 14: Transformation Matrix (B)
As an aside, the option to have local element declarations makes XSD Schema more descriptive than XML DTD.
[TODO: Discuss the substitution principle.]
Limitations of the Russian Doll schema
The previous theorem demonstrates the strength of the Russian Doll pattern that stems from its local element declarations and that makes it incongruent with the Salami Slice and Garden of Eden patterns, which have mandatory global element declarations.
In contrast, the combination of local element declarations with local type definitions determines a weakness of the Russian Doll pattern compared to any of the other three patterns.
Proposition The instances of a Russian Doll schema are limited in height by the height of the schema.
We prove the proposition at the end of this subsection.
None of the other three schemas have that property.
Let us look at the documents docAi that we have introduced by example above, for
any natural number i. The document docAi has only element nodes that are
named a and no text nodes. The depth of docAi is i
and an element node in docAi has either 0 or 1 child node(s). Hence, docAi
is a chain of element nodes a of depth i.
We collect all the documents docAi into the language langA. It is
easy to see that langA is the language of a Garden of Eden schema, of a
Salami Slice schema and of a Venetian Blind schema. Examples of such schemas are
defined below.
Figure 15: Salami Slice schema for langA
Figure 16: Venetian Blind schema for langA
Figure 17: Garden of Eden schema for langA
It follows from the proposition above, that langA is not the language
of any Russian Doll schema. Hence, we can make the weakness of the Russian Doll
pattern explicit.
Theorem VB, SS, GE are each incongruent with RD.
Figure 18: Transformation Matrix (C)
We still have to prove the proposition above. For that, we simply verify from the definition of validity, that for each instance of a Russian Doll schema, each element node of the instance is valid with respect to an element declaration of the same schema that has the same depth.
This concludes the proof of the theorem.
From global to local
After highlighting the power of local element declarations and their expressive power, we might think that converting from global element declarations or type definitions to local ones should be easy. There must be a snag, though, when considering this direction. We know already that VB is incongruent with RD, so it doesn't seem to be possible to make global type definitions local. And since SS is inconsistent with VB, it doesn't seem to be possible to make global declarations local. In both cases, we have achieved impossibility results by considering the height of instances of RD schemas. Let us find out, if there are conditions under which we might be able to turn global components into local ones.
Let us first look at global type definitions. As we have discussed, we can take a single reference to a global type definition and replace it with a copy of the global type definitions, without the name, and the instances of the schemes before and after the transformations have not changed. The issue is that we might have introduced a new reference to the same type definition that then would also have to be replaced, and so on, ad infinitum.
We demonstrate that phenomenon with the Venetian Blind scheme for
language langA that we have presented above. If we replace a
reference to the global type definition with a local copy, we introduce a new
reference to the same global type definition, and we will never be able to eliminate
the global type definition if we continue this way.
Figure 19: Rewritten Venetian Blind schema for langA
The same phenomenon occurs if we attempt to replace references to global element
declarations with local declarations, as illustrated by the Salama Slice schema
for
language langA.
Figure 20: Rewritten Salami Slice schema for langA
The problem in both cases is recursion that cannot be eliminated by unrolling it. Our examples have simple recursions where a global type definition or a global element declarations contains a reference to itself. Of course, there could also be indirect references that are not as easy to detect at first glance. They would have the same problem.
[TODO clarify, this is cryptic] Solution through the striped pattern of element declarations refering to type definitions refering to element declarations.
Let us assume that we have a Garden of Eden schema, in which all element declarations and all type definitions are global. Each element declaration is global, and it references a global type definition; also, each type definition is global, and in its content model it only talks about global element declarations through references.
If we make a complex type definition local by copying it into an element declaration that references it, we do not copy any references to type declarations. Hence, since there are only finitely many references to type definitions in the original schema, after finitely many steps we have eliminated all references to global type definitions in the schema, so we can remove the global type definitions. We end up with a Salami Slice schema, as witnessed by the following figure.
Figure 21: Garden of Eden schema for langA, rewritten as a Salami Slice
schema

If we make an element declaration local by copying it into a type definition that references it, we do not copy any references to element declarations. Hence, since there are only finitely many references to element declarations in the original schema, after finitely many steps we have eliminated all references to global element declarations in the schema. We leave the original global element declaration in the schema as entry points for instances, but they are no longer referenced. We end up with a Venetian Blind schema, as witnessed by the following figure.
Figure 22: Garden of Eden schema for langA, rewritten as a Venetian
Blind schema

We have just proved that SS and VB are both more powerful than GE. Taking into account a previous result that GE is more powerful than SS, by transitivity, we can also conclude that VB is more powerful than SS. This implies the following theorem:
Theorem SS and VB are both more powerful than GE. VB is more powerful than SS.
Figure 23: Transformation Matrix (D)
From an earlier investigation, we know that we can transform an arbitrary XSD schema into one that has only global type definitions. In a next step, we can replace all references to global element declarations with local element declarations. This results in a Venetian Blind schema. Hence, VB is more powerful than U. Since each schema in VB is also in U, we conclude:
Theomem
VB and U are equally powerful.
All results from this section are summarized in Figure 11, which is an overlay of all diagrams in this section.
Conclusion
We have clarified the relationship between the four schema classes RD,
GE, SS and VB in terms of descriptive
power. It turns out that VB is strictly more powerful than any of the other
three classes, and that it is equally powerful to the universal set of XSD
schema U. The classes RD and SS are
incomparable, and so are RD and GE. Finally,
GE and SS are equally powerful. This characterizes
the power relationship between all six (unordered) pairs of the four schema classes
and
the patterns that define them, as illustrated in Figure 11.
Global element declarations and type definitions can be re-used within an XSD schema and also between different XSD schemas. Local element declarations and type definitions are encapsulated within the type definitions respectively element declarations to which they belong. They are only visible within these parent constructs and cannot be re-used. Hence, XML Schema gives schema designers the flexibility to satisfy specific requirements of re-use and encapsulation when designing an XSD schema.
The pattern that has the most descriptional power, namely Venetian Blind, allows for re-use of type definitions but not of element declarations. If the use of inheritance and of substitution groups is desirable [BST2007], then at least some type definitions and element declarations need to be global. This is an argument for the Garden of Eden pattern or for a hybrid pattern that is partially Garden of Eden and partially Venetian Blind. A pure Garden of Eden pattern loses the option of local element names.
Further patterns in XML schemas that take into account namespaces and inheritance, for example the Chameleon pattern and double extension. Relate this work to more general discussion on patterns and good practices for XML Schema and other schema languages. [W2013, T2002, V2002, C2006a, B2010]. To incorporate this work probably requires extension of the model for schemas.
Patterns in Relax NG. Named element declarations (decoupling names of declarations from names of elements). This requires extension of the model for schemas.
Patterns and tools: It seems that the XML tools of the IDE Netbeans offer to translate between any of the four patterns, as described on the Oracle web site [KS2006]. That text is in itself shaky. It explains patterns in terms of element declarations, with tenuous connections to type definitions; and it looks at examples that supposedly follow the RD patterns but are actually VB. Oxygen and possibly other tools correctly convert XML DTDs to Salami Slice XML schemas. It is worth to investigate systematically how tools handle schema patterns.
What is the distribution of patterns in practice? Investigate prominent schemas and provide statistics.
References
[B2010] James Bean. XML Schema Design
Patterns.
In James Bean (editor), SOA and Web Services Interface
Design, pp 211-234. Morgan Kaufmann, 2010.
[BD09] Bernd Brügge; Allen Dutoit. Object-Oriented Software Engineering Using UML, Patterns, and Java. Prentice Hall, 2009.
[BPS2008] Tim Bray; Jean Paoli; C.M.
Sperberg-McQueen; Eve Maler; François Yergeau. Extensible Markup Language (XML)
1.0 (Fifth Edition).
[online]. [cited 19 March 2020].
http://www.w3.org/TR/2008/REC-xml-20081126/.
[BST2007] Anne Brüggemann-Klein;
Thomas Schöpf; Karlheinz Toni. Principles, Patterns and Procedures of XML Schema
Design — Reporting from the XBlog Project.
Extreme Markup Languages 2007
(Montréal, Québec). [online]. [cited 22 March 2020].
http://conferences.idealliance.org/extreme/html/2007/BruggemannKlein01/EML2007BruggemannKlein01.html.
[C2006a] Roger L. Costello (for
xml-dev list). XML Schemas: Best Practices.
[online]. [cited
11 April 2020]. http://www.xfront.com/BestPracticesHomepage.html.
[C2006b] Roger L. Costello (for
xml-dev list). Global versus Local — A Collectively Developed Set of Schema
Design Guidelines.
[online]. [cited 22 March 2020].
https://www.xfront.com/GlobalVersusLocal.html.
[GST2012] Shudy (Sandy) Gao; C.M.
Sperberg-McQueen, Henry S. Thompson. W3C XML Schema Definition Language (XSD) 1.1
Part 1: Structures.
[online]. [cited 19 March 2020].
http://www.w3.org/TR/2012/REC-xmlschema11-1-20120405/.
[KS2006] Ayub Khan; Marina Sum.
Introducing Design Patterns in XML Schemas.
[online]. [cited
22 Month 2020].
https://www.oracle.com/technetwork/java/design-patterns-142138.html.
[M2002] Eve Maler. Schema
Rules for UBL... and Maybe for You.
[online]. XML 2002 Conference. [cited
22 March 2020].
http://www.ebxml.org/presentations/ubl-schema-rules-xml2002.pdf.
[P2015] Saumil Patel. XML
Schema Design Patterns.
[online]. [cited 22 March 2020].
https://saumilp.github.io/posts/xml-schema-design-patterns/.
[T2002] Jeni Tennison. Jeni's
Schema Pages.
A Tutorial presented at Extreme Markup Languages 2002.
[online]. [cited 11 April 2020] http://www.jenitennison.com/schema/>.
[V2002] Eric van der Vlist. XML Schema. Kindle edition. O'Reilly Media, 2002.
[W2013] Priscilla Walmsley. Definitive XML Schema. 2nd edition (Kindle). Prentice Hall, 2013.
[WSC2017] Norman Walsh; John Snelson; Andrew
Coleman. XQuery and XPath Data Model 3.1.
W3C Recommendation 21 March
2017. [online]. [cited 12 April 2020].
https://www.w3.org/TR/2017/REC-xpath-datamodel-31-20170321/.
[1] A content model references a global element declaration by its name. A local element declaration is contained within the content model; it cannot be accessed from outside the content model.
[2] Of course, the depth of an XML document and of an XML schema is just the usual depth of the tree that is defined through the consists-of relationship, so the two domain-specific definitions could be unified into a more general definition.