Existing data structures for strings
In this section I outline several existing ways of representing strings,
with the advantages and disadvantages of each.
Monolithic char arrays
Java and C# represent a string as an array of 16-bit char units,
in contiguous memory. A character above the 16-bit limit (a so-called
astral character) is represented as a surrogate pair: that is,
a sequence of two 16-bit numbers in a reserved range. This means that
the number of bits per Unicode codepoint is variable (16 or 32), which
in turn means that Unicode codepoints are not directly addressible.
Since Java 9, strings consisting entirely of 8-bit characters use an
optimized representation that allocates 8 bits per character rather than 16.
This creates a discontinuity: the space occupancy of a long string doubles
as soon as it contains a single non-ASCII character. It also increases the cost
of string concatenation if one of the operands needs to be widened from an 8-bit
to a 16-bit representation.
The main disadvantages are:
-
Maximum string length of 231 characters
-
Not codepoint-addressable
-
String concatenation requires copying of the operand strings, even
though they are immutable
-
Operations such as replace() require copying the unchanged parts of the
string as well as the changed parts.
Building a large string incrementally in Java with a sequence of string concatenation
operations
notoriously has O(n2) performance, and to counter this, the language
offers a mutable StringBuilder class to hold a string temporarily while under construction.
This is fine to underpin some XPath operations such as string-join(), where there’s no problem using a mutable
data structure transiently during the execution of the function. But it doesn’t work
where the user
application constructs a string incrementally, for example by use of a recursive function
or by a
fold-left() operation. In such cases each intermediate string needs to be fully accessible at
every stage
of processing, and immutable, so update operations such as concatenation are not allowed
to modify their operands.
Strings in Saxon
In the Saxon XSLT processor (at any rate, the version built using Java
as the implementation language), a number of techniques are used to
mitigate the disadvantages of the native string representation:
-
In some situations (for example, regular expression processing and
the translate() function) strings are expanded temporarily to an
array of 32-bit integers, to provide codepoint addressibility.
-
XDM string values are wrapped in an object that contains additional
information about the string (for example, its XDM type). This
additional information includes a bit that indicates when a string
is known to contain no surrogate pairs; if this bit is set, XPath operations
like substring() can be performed more efficiently, because they map directly
on to underlying Java operations.
-
Many internal interfaces use the CharSequence interface rather than
java.lang.String. The CharSequence interface allows alternative
representations of strings, including user-defined implementations.
Saxon uses a number of custom implementations of CharSequence including:
-
CharSlice, which is a view of a portion of a char array
(useful for capturing the char array passed over by an XML
parser implementing the SAX interface; but dangerous because
the char array is mutable both in theory and in practice).
-
CompressedWhitespace, a compressed representation of the
whitespace text nodes that typically occur between XML elements:
compression is achieved using run-length encoding.
-
FastStringBuffer, an implementation designed to allow efficient
in-situ appending to a string. Again dangerous because it is mutable.
Use of the CharSequence interface doesn’t solve all our problems.
It’s still limited to 231 characters;
and it still isn’t codepoint-addressable.
What it does achieve is to reduce the amount of copying required by
some operations, such as substring().
Saxon implements XDM node structures using a data structure called the TinyTree.
This economises on space by avoiding the traditional one-Java-object-per-node
tree design, and provides fast searching by representing node names
in the tree as a single array of integer name codes. (If a document contains
one million nodes, then searching for an element by name reduces to a sequential
search of a contiguous array of one million 32-bit integers, which is extremely fast
as a result of CPU caching: often faster than using an index.)
Text nodes in the tiny
tree are represented using integer offsets into a LargeTextBuffer structure
which is an array of fixed-length segments. Each segment except the last
is exactly 65535 Unicode characters in length; segments represent characters
using 8, 16, or 24 bits per character depending on the highest codepoint
present in that segment. This achieves Unicode codepoint addressibility.
In principle it allows more than 231 characters in a string, but we don’t
actually exploit this because it uses 32-bit int values for addressing, and
because many operations require XDM strings to be converted to Java strings.
One of the original ideas was that the characters representing the string
value of a non-leaf element (defined as the concatenation of its descendant
text nodes) would be directly available as a contiguous section of the
LargeTextBuffer, but again, we don’t actually exploit this capability,
largely because of the complications caused by compressed whitespace text
nodes. When an operation calls for atomization of an element or text node,
we represent the result as a CharSequence: if the characters needed are
contiguous in a single segment, we avoid any copying operations, but if the
value spans segments, we make a copy.
One of the disadvantages of the extensive reliance on the CharSequence
interface is that it has no equivalent in the C# language. The way in
which we derive Saxon products for both the Java and C# platforms from
a single code base [Kay 2021] is beyond the scope of this paper; but the requirement
to do so means that we make our life easier if we confine ourselves to
functionality available in both languages.
The overall effect of these various techniques has been to give reasonably
good all-round performance. But the limitations mean that we have been
looking for something better.
Ropes
A relatively little-known data structure for handling strings is the rope
[Boehm, Atkinson, and Plass 1995].
A rope represents a string as an immutable binary tree of short segments.
Typically each non-leaf node in the tree represents a substring of the overall
string, and contains pointers to left and right substrings, plus a length field.
Substring operations extract a subtree; concatenation forms a supertree.
Operations such as replace() can reuse parts of the original
string that are unaffected by the change, without copying. The structure thus
affords a good solution for most of the requirements, including addressibility,
scaleability, and immutability without excessive copying.
The main problems are keeping the tree balanced, and preventing excessive
fragmentation. The definitive paper on ropes sketches an algorithm for keeping
the tree balanced, but it makes no attempt to prevent fragmentation: specifically,
a string built by appending a large number of small substrings will not be
consolidated into a smaller set of larger substrings, which means that the number
of objects used to represent the tree can become very large, and the depth of
the tree can also grow to an uncomfortable level. A fragmented tree also leads
to poor locality of reference and therefore poor CPU cache effectiveness.
Finger Trees
A finger tree [Hinze and Paterson 1995] is
a flexible functional data structure used to represent ordered sequences or lists.
It’s designed
to provide efficient implementation of a broad range of operations including insertion,
deletion,
scanning, and searching; a particular characteristic compared with other tree representations
is
that the tree is shallower at its extremes, and deepest in the centre, which makes
addition of entries
at either end of the sequence particularly efficient.
Although strings are sequences of characters, general purpose list structures are
not well suited
for storing strings because of the space overhead, and because of the need for locality
of reference
(which implies using contiguous storage for adjacent characters where possible). Of
course a rope,
as described in the previous section, is a tree of substrings, and there is no reason
why this tree should
not be implemented as a finger tree.
But any structure that maintains strings as a list of substrings needs to consider
how and when
adjacent substrings should be consolidated. As mentioned above, the literature on
ropes has little
to say on this subject, and implementing the tree as a finger tree doesn’t solve the
problem.
The key idea with finger trees, which are shallower at the extremities to provide
extra efficiency for
prepend and append operations, suggests that a similar idea might be applied to the
consolidation
of substrings within a rope structure, namely using shorter segments at either end
of the string.
This is the principle of the ZenoString structure presented in the next section.
ZenoStrings
The ZenoString is a proposed representation for strings that takes
inspiration from a number of existing sources, but which (as far as the author can
tell)
is otherwise novel.
A ZenoString is essentially a list of string segments. The segments can be different
lengths, and they
can use different string representations internally. The objects in the top-level array
contain two fields:
In pseudocode, we can express the data structure as:
ZenoString = {Entry[]};
Entry = {int64 offset, Segment segment};
Segment = {int24[] characters}where X[] represents a list or array whose entries are of type X,
int64 represents a 64-bit integer, and int24 represents
a 24-bit Unicode codepoint; fewer bits per character are used where possible,
but the characters in a segment all use the same representation.
The structure can be seen as an implementation tree of constant depth 3: the root
is represented implicitly
by the ZenoString object; the nodes at the second level are the entries, and the nodes
at the third
level are the individual characters.
To find the character at a particular position, the relevant segment
can be located by a binary-chop search of the top-level list of entries. To extract
the substring of characters between two given positions, a new ZenoString
can then be formed by constructing a new top-level array of entries, making a partial
copy of segments that are partially included in
the result, and reusing segments, without copying, if they are included in the
result in their entirety. (In our implementation, we represent the result of a substring
operation using a simpler data structure if it contains only one segment.)
To concatenate two ZenoStrings, in principle it is merely necessary to
copy the entries in the two top-level arrays, adjusting the segment offsets as appropriate.
The underlying segments can be reused, since they are immutable.
However, this would lead to fragmentation when a string is built by
incremental concatenation. We therefore take the opportunity at this
stage to perform some consolidation to reduce the number of segments.
Our first-cut algorithm for consolidation is to apply the following rule:
If the length of any segment other than the last
is less than or equal to the length of its right-hand neighbour,
then combine the two segments into one.
To examine the effect of this rule, consider first the case where
single characters are appended at the right hand end of the string.
The string will tend towards a structure containing log2(N) segments
where N is the length of the string, with the longest segments near
the start: for example segments of length (256, 128, 64, 32). When we add 26 individual characters to build up a string, the effect is demonstrated
by the sequence below:
A
AB
AB C
ABCD
ABCD E
ABCD EF
ABCD EF G
ABCDEFGH
ABCDEFGH I
ABCDEFGH IJ
ABCDEFGH IJ K
ABCDEFGH IJKL
ABCDEFGH IJKL M
ABCDEFGH IJKL MN
ABCDEFGH IJKL MN O
ABCDEFGHIJKLMNOP
ABCDEFGHIJKLMNOP Q
ABCDEFGHIJKLMNOP QR
ABCDEFGHIJKLMNOP QR S
ABCDEFGHIJKLMNOP QRST
ABCDEFGHIJKLMNOP QRST U
ABCDEFGHIJKLMNOP QRST UV
ABCDEFGHIJKLMNOP QRST UV W
ABCDEFGHIJKLMNOP QRSTUVWX
ABCDEFGHIJKLMNOP QRSTUVWX Y
ABCDEFGHIJKLMNOP QRSTUVWX YZ
After appending 19,999 individual characters, the
segment lengths will be (16384, 2048, 1024, 512, 16, 8, 4, 2, 1), while with one million
characters the lengths will be (524288, 262144, 131072, 65536, 16384, 512, 64).
In fact the very short segments at the end serve no useful purpose, so to avoid short
segments we refine the rule
as follows:
If the length of any segment other than the last
is less than or equal to the length of its right-hand neighbour,
or if the combined length of the two segments is less than 32,
then combine the two segments into one.
With this rule, a string built by appending 19,999 individual characters has
segments with lengths (16384, 2048, 1024, 512, 31), while with a million characters
the lengths are now (524288, 262144, 131072, 65536, 16384, 512, 32, 32)
The significance of having shorter segments near the end, where new
data is likely to be added, is that adding a new character to an existing
segment is cheaper if the segment is short, because it reduces the amount of
character copying. But we don’t want all the
segments to be short, because that increases the per-object space overhead,
increases the length of the search needed for substring operations, and reduces
locality of reference when processing the entire string.
The key operations on a ZenoString perform as follows:
-
Scanning the string: O(n). This simply involves scanning each of the segments in turn.
Note that the cost of scanning is for practical purposes independant of the the number
of segments
or their size distribution.
-
Finding the Nth character of the string
(or a substring from positions M to N): O(log N). The relevant
segment or segments can be found by a binary chop on the index array. The operation
of extracting a substring
has already been discussed.
-
Searching for a substring: O(n). The positions where a particular
character occurs can be obtained by scanning the string looking for that character;
to search
for a substring (needed for example to support contains()), search for the first
character, then scan forwards to compare the subsequent characters with those of the
required substring.
-
Appending a character: O(1). This either involves creating a new segment, or adding the character
to the last segment. It may also involve some consolidation of preceding segments,
but this is
sufficiently rare that it does not contribute significantly to the cost. During string
construction
each character is copied log(N) times where N is the
final length of the string.
-
Inserting or removing a character or substring other than at the end: O(N).
If the position of the insertion or removal is random, then on average a little over
25% of the
characters in the existing string will need to be moved, on the assumption that the
largest segment contains half
the string, and inserting or removing into this segment involves moving all the characters
in this segment. So
50% of the time, 50% of the characters will need to be moved; 25% of the time, 25%
will need to be moved, and so on,
giving the overall average number of character moves as N × (1/4 + 1/16 + 1/64...).
-
Concatenating two strings: O(1). In the simplest case this just involves copying the index arrays and
adjusting the offsets accordingly (the actual segments can be reused, they do not
need to be copied).
There is the option of consolidating the segments to reduce fragmentation: this is
discussed below, but it is not
an expensive operation.
If, instead of appending characters one at a time, a string is built incrementally
by appending strings that
are less predictable in length, the segment lengths will follow the same general
pattern, but without such perfect regularity. For example if we build a string by
concatenating the words of
Shakespeare’s Othello (one word at a time), we get a string with segment lengths
(93820, 25652, 2667, 233, 215, 118, 64, 61, 26, 13).
Of course, appending short strings to a long (and lengthening) string is not the
only use case to consider. Several other use cases for string concatenation in particular
are worth considering:
-
Building a string by successive prepend operations.
-
Concatenating two large strings, each containing multiple segments.
-
Replacement of internal substrings: for example using the replace() operation
to match short substrings and replace them. (This was in fact the use case that
motivated this research.)
The problem for incremental prepend is that the rule proposed earlier always results
in the entire
string occupying a single segment. To tackle this case we can modify the rule for
merging adjacent segments
as follows:
If any segment other than the first or last
is shorter than or equal to both its neighbours,
or if the combined length of the segment and its right-hand neighbour is less than
32,
then combine the segment with its right-hand neighbour.
The effect of this rule is to create a sequence of segments with short segments at
both ends, and longer
segments in the middle. When we build the text of Othello by appending individual
words we now get segment lengths of:
(29, 57, 62, 119, 133, 141, 365, 1193, 2422, 2455, 6835,
9420, 15864, 23299, 31426, 25652, 2667, 233, 215, 118, 64, 61, 26, 13)
And when we build it by prepending one word at a time the segment lengths are:
(13, 46, 86, 168, 411, 826, 2021, 3486, 4209, 4353, 10873, 16147, 43964,
29580, 2105, 1428, 1010, 923, 586, 234, 164, 116, 64, 56)
So in both cases we end up with a sequence where the segments near the ends are shortest,
meaning that the
bulk of the existing segments can be reused when data is added at either end.
How does this work for the general case of concatenating two strings of arbitrary
length? If the two strings are ZenoStrings, then we would expect the final segments
of the
first operand, and the initial segments of the second operand, to be quite short,
and a natural
strategy is to coalesce the short segments in this region into one larger segment.
This situation arises in the course of implementing the replace()
function. If we choose, for example, to replace all occurrences of "'d" in Shakespeare’s
Othello by "ed"
(so "embark'd" becomes "embarked", and "call'd" becomes "called"), this is likely
to result in a sequence of concatenations,
with the operands being long substrings of the original text (average length around
1000 characters)
interspersed with occurrences of the short 2-character replacement string. Is it better
to leave
the short replacement strings as individual unconsolidated segments in the result,
or is it better
to combine them with their neighbours to reduce the fragmentation of the string? The
answer is,
it depends on how the string is subsequently used.
In fact there is no need to use the same consolidation algorithm after every operation;
we could
use right-consolidation (producing shorter segments at the right hand end) after
appending a short string, and left-consolidation (producing shorter segments at the left hand end)
after prepending a short string. In each case we are optimising the resulting string
on the assumption that a sequence
of similar operations is likely to follow. The downside of this approach, however,
is that consolidation is no
longer idempotent, which creates the risk that a sequence of dissimilar operations
will cause expensive oscillation
between two different states. A solution to this might be to perform only local consolidation
after each operation
(confined, say, to the first or last few segments) until the string as a whole crosses
some threshold, such as having
more than P segments whose length is less than Q, for suitable values of P and Q.
Strings, like most other data structures, tend to have phases of processing in which
they are subject to frequent
modification, and phases in which they are largely read-only. Modifying strings is
fastest when the string is more fragmented,
and using the string is fastest when it is less fragmented. This calls for an adaptive
approach in which consolidation
operations respond to the usage pattern.
Another factor that could influence how best to consolidate strings is the variable
width of characters.
Segments can be implemented as contiguous arrays using a constant number of bits
per character (8, 16, or 24) depending on the largest codepoint appearing
in the segment. A possible variation is to avoid merging segments if their
character widths differ, but I have not explored the effect of this.
It is also possible to refrain from merging segments beyond some maximum
length (say 16M characters) to make it easier for the underlying memory
management to allocate suitable memory segments, at the cost of making
substring operations on very large strings take rather longer.
Performance
No paper that proposes a new data structure or algorithm would be complete without
a section
demonstrating that the innovation delivers measurable performance benefits.
Demonstrating this, however, is easier said than done. We need to decide what to measure,
and we need
to decide what to compare it with.
In choosing what to measure, we need to convince the sceptical reader that we have
not simply
chosen a use case that demonstrates the technique in ideal circumstances, and that
the benefits
for this use case do not result in hidden costs elsewhere. We also need to be aware
of
Goodhart’s Law:
When a measure becomes a target, it ceases to be a good measure. The point
here is that when we choose one particular workload to demonstrate the superior characteristics
of the algorithm, we will naturally tend to tweak the algorithm to optimise its performance
for that particular task, regardless of whether these adjustments have any effect
(either beneficial or adverse)
on other tasks that might be equally important, but which are not being measured.
We also need to consider what baseline to use for comparison.
The use case that motivated this study was a transformation that performed multiple
string replacements on an input text. The string replacements were taken from a supplied
dictionary, and were variable in number: imagine, for illustration, that all English
spellings
of German cities are to be replaced with their local spellings, so Cologne
becomes Köln, Nuremberg becomes Nürnberg,
Brunswick becomes Braunschweig, and so on.
One approach is to take this as the definitive use case, and measure the effect
of the algorithm on this particular transformation. But it’s not as simple as this:
-
The results depend greatly on the length of the text, and the number of replacements
to be performed. They are also sensitive to details such as the incidence of characters
requiring
8, 16, or 24 bits for their Unicode codepoints. In particular, we know if we take
the existing
Saxon product as our baseline, then there are worst-case scenarios involving input
strings
with surrogate pairs. Should we include such scenarios in our baseline, given that
we know
they are rare?
-
While working on this problem, optimizations were found that have little to do with
the
new data structure or algorithm. The biggest benefit was to change the implementation
of replace() so that in cases where there is no match on the replacement string, the input string
is returned unchanged. Should our baseline include this optimization, or not?
-
After the sequence of replacements is complete, the degree of fragmentation in the
resulting string affects the performance of subsequent operations on that string.
How can we construct a benchmark that takes this into account?
-
What should we compare with? Should we compare Saxon using ZenoStrings with the
released Saxon product? Or should we produce an alternative implementation that
enhances Saxon to use Ropes, and use that as the baseline for comparison?
There is no definitive right answer to any of these questions.
Despite all these caveats, we can only have confidence in the algorithm if we measure
something,
and I have chosen two benchmarks which I hope will yield useful insights. They are
presented in
the next two sections.
Case Study: Dictionary-based Word Substitution
The first task I propose to measure is as follows: for a sequence of a dozen or so
pairs of short strings (X, Y),
replace all occurrences of X in a text of moderate length by Y. For our input text
we’ll use the text
of Shakespeare’s Othello, and for our replacement strings we’ll take the dramatis personae (Othello,
Desdemona, Iago, Emilia, etc: eleven names in total), and wrap these names in square
brackets so they become [Othello],
[Desdemona] etc. So Roderigo’s line Is that true? why, then Othello and Desdemona
return again to Venice becomes Is that true? why, then [Othello] and [Desdemona]
return again to Venice.
Note: this task is not the one for which the design of ZenoStrings is optimized: changes
to the content
of a string can occur anywhere within the string, so there is no particular benefit
from having short segments at the
string’s extremities.
We can express this task using the following XPath 3.1 implementation (where $text is
the input text, as a single string):
let $personae :=
('Othello', 'Desdemona', 'Iago', 'Emilia',
'Brabantio', 'Gratiano', 'Lodovico', 'Cassio',
'Roderigo', 'Montano', 'Bianca')
return fold-left($personae, $text, function($str, $persona) {
replace($str, $persona, '[' || $persona || ']')
}Now, it happens that under the released product Saxon 10.5, this query gives perfectly
acceptable performance
when we use the system function fn:replace() to do the string replacement. It executes in an average of
12.8ms, using peak memory of 320Mb. If we expand the source document from 250Kb to 2.5Mb
(ten copies of Othello concatenated end-to-end),
it still executes in 88ms, with a similar memory requirement. That's because fn:replace(),
being a system function, already optimizes the way it assembles the result string
by using a mutable Java StringBuilder
internally.
Trying to improve this using a ZenoString internally (in the hope of saving time or
space by reusing the long substrings
that are copied unchanged from the input to the output) turns out to give no benefits:
on the contrary, execution time increases
to 14.5ms in the 250Kb case and 392ms in the 2.5Mb case.
This changes if, instead of using the system function fn:replace, similar logic is implemented in user code,
for example using the XQuery 3.1 function:
declare function local:replace($text, $old, $new) {
if (contains($text, $old))
then substring-before($text, $old) || $new ||
(substring-after($old) => local:replace($old, $new))
else $text
};(It’s easy to find a slight variation in the requirements that would necessitate such
logic: for example, changing
all the matched strings to upper-case is beyond the capabilities of fn:replace().)
In fact with a large number of matches, this user-written function fails with a stack
overflow
exception because it recurses too deeply.
We can avoid this problem by rewriting it to take advantage of tail call optimization:
declare function local:replace($text, $old, $new) {
local:replace2("", $text, $old, $new)
};
declare function local:replace2($left, $right, $old, $new) {
if (contains($right, $old))
then local:replace2($left || substring-before($right, $old) || $new,
substring-after($right, $old), $old, $new)
else $left || $right
};Using the released product Saxon 10.5, this query takes 29.8ms.
When we scale up the source document from 250Kb to 2.5Mb, the elapsed time increases
rather dramatically to 1911ms.
With ZenoStrings used to hold intermediate results, the elapsed time drops to 11.2ms
for the 250Kb document,
537.4ms for the 2.5Mb case: around three times as fast. Furthermore, Saxon 10.5 shows
peak memory usage of 550Mb,
while the ZenoString solution is steady at around 300Mb.
Analyzing the behaviour of the two implementations (one using the system function
fn:replace(),
one using a home-grown alternative), it’s not hard to see why the ZenoString implementation
should deliver benefits
only in the second case.
-
With fn:replace(), every unchanged character in the input is being copied 11 times,
once for each call on fn:replace(). So the total number of characters being copied
is about 1.35M (or 13.5M with the larger text), and they are copied in large contiguous
chunks
so the action is highly efficient. This is not enough of a problem for
ZenoStrings to deliver any benefits. The solution scales linearly for the larger input
text.
-
With Saxon 10.5 using the home-grown recursive replace function, every unchanged character
in the input is being
copied on average 11 × N times, where N is the average number of occurrences of the
personae names in the input text (around 30 in the shorter text, 300 in the longer).
This shows why the solution does not scale linearly: for the 250Kb text we
copy 250,000 × 11 × 30 = 82.5M characters; for the 2.5Mb text the number is 2,500,000
× 11 × 300 =
8.25G characters.
-
With ZenoStrings, again using the home-grown recursive replace function, it is harder
to
calculate the number of character copying operations, as it depends on the detailed
operation
of the consolidation algorithm. However, internal instrumentation shows that consolidation
of ZenoStrings accounts for copying of 1.2M characters (in 128 chunks) for the smaller
input document, and
18.9M (in 847 chunks) for the larger document. Because of CPU caching effects, the
number of
chunks being copied is probably more signficant than the size of the chunks. But note
that the number
of characters being copied is not growing quadratically with the size of the input,
as it does in the
Saxon 10.5 solution.
For what it’s worth, the final result of the ZenoString solution (as currently implemented),
is
a ZenoString with segment lengths (25, 501, 16295, 24987, 30408, 39241, 21561, 16868,
4747) for the shorter
input text, and (25, 501, 16295, 24987, 30408, 39241, 59997, 154633, 309266, 618532,
154633, 55395, 39241, 21561, 16868, 4747)
for the longer.
Case Study: Word-wrap
The second task chosen for performance benchmarking is word-wrapping of text: that
is, taking
an input string and arranging it in such a way that each word is added to the current
line if it
fits within some maximum line length, or placing it on a new line otherwise.
Once again I’ve written the code to take advantage of tail-call optimisation, so it
reads like this:
declare variable $NL := codepoints-to-string(10);
declare function local:wordwrap($text, $lineLength) {
local:wordwrap2("", tokenize($text), 0, $lineLength)
};
declare function local:wordwrap2($result, $tokens,
$currentLineLength, $maxLineLength) {
if (empty($tokens))
then $result
else if ($currentLineLength + string-length(head($tokens)) ge $maxLineLength)
then local:wordwrap2($result || $NL || head($tokens),
tail($tokens),
string-length(head($tokens)),
$maxLineLength)
else local:wordwrap2($result || ' ' || head($tokens),
tail($tokens),
$currentLineLength + string-length(head($tokens)) + 1,
$maxLineLength)
};
local:wordwrap($input, 80)For readers unfamiliar with XQuery, tokenize() splits a string on whitespace
boundaries returning a sequence of strings; || performs string concatenation, head()
and tail() return the first item in a sequence, and the remainder of the sequence, respectively;
string-length() returns the length of a string in Unicode codepoints; empty()
tests whether a sequence is zero-length.
We’ll exercise this code by running it with samples of Lorem Ipsum text
of different lengths (measured in words, defined here as space-separated tokens).
The text is
all lower-case ASCII alphabetic characters.
For short input texts (texts that are representative of the paragraphs that are likely
to be
word-wrapped in a real publishing application), the performance is excellent with
both the conventional string
representation in Saxon 10.5, and with the new ZenoString code. In both cases it appears
to scale linearly
with the length of the text, and the ZenoString gives an improvement that is around
a factor of two:
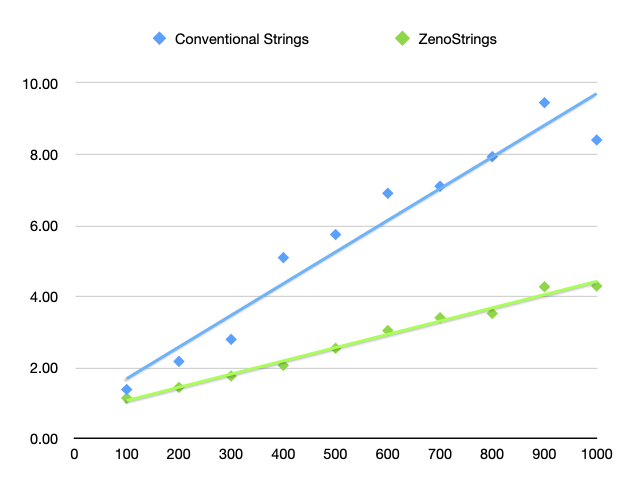
Table I
Time (in ms) to word-wrap inputs of 100 to 1000 words
| Length of text (words) |
Conventional strings |
ZenoStrings |
| 100 |
1.38ms |
1.14ms |
| 200 |
2.17ms |
1.44ms |
| 300 |
2.79ms |
1.76ms |
| 400 |
5.09ms |
2.06ms |
| 500 |
5.74ms |
2.54ms |
| 600 |
6.90ms |
3.04ms |
| 700 |
7.10ms |
3.40ms |
| 800 |
7.93ms |
3.52ms |
| 900 |
9.45ms |
4.27ms |
| 1000 |
8.40ms |
4.29ms |
Further investigation, however, shows that the apparent linear scaleability is an
illusion. There is actually
a quadratic element to the cost: the elapsed time can be expressed as
Equation (a)
a + bx + cx2
where
c is sufficiently small that the last term is insignificant for small values of
x.
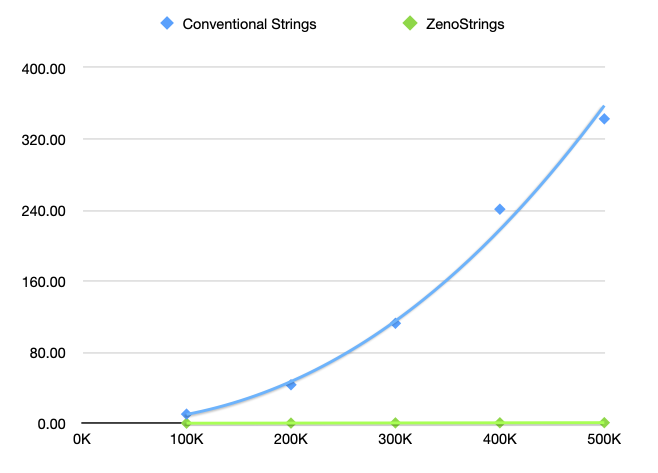
The quadratic effect shows up when we measure the performance for larger input strings:
Table II
Time (in seconds) to word-wrap inputs of 100K to 500K words
| Length of text (words) |
Conventional strings |
ZenoStrings |
| 100K |
10.31s |
117ms |
| 200K |
43.32s |
228ms |
| 300K |
112.5s |
429ms |
| 400K |
240.9s |
563ms |
| 500K |
342.6s |
699ms |
The quadratic element arises from the cost of string concatenation. On each recursive
call of the wordwrap
function, we are adding one token to the result string, and with the conventional
approach, this involves
copying the existing string, which has a cost proportional to the length of the string.
With the ZenoString,
concatenation has constant cost, which eliminates the quadratic element of the total
elapsed time
of the query.
In this case study, ZenoStrings show only a modest benefit for workloads that are
likely to be
encountered in everyday practice. But the case study also shows that they can deliver
very substantial
improvements for more extreme workloads; and perhaps as importantly, that the additional
complexity
does not cause any problems when applied at the smaller scale.
Unlike the previous case study, this task plays to the ZenoString’s strengths: because
we are
repetitively adding small increments at the end of a long string, the consolidation
algorithm’s policy
of leaving the shortest segments at the right-hand end of the string leads directly
to the improved
bottom line in query execution time. However, we've resisted the temptation to tweak
the algorithm
to give even better results: we could exploit the fact nothing is being done with
the wordwrapped
string other than to send it to the serializer, but we haven't done so.