How to cite this paper
Tovey-Walsh, Norm. “Ambiguity in iXML: And How to Control It.” Presented at Balisage: The Markup Conference 2023, Washington, DC, July 31 - August 4, 2023. In Proceedings of Balisage: The Markup Conference 2023. Balisage Series on Markup Technologies, vol. 28 (2023). https://doi.org/10.4242/BalisageVol28.Tovey-Walsh01.
Balisage: The Markup Conference 2023
July 31 - August 4, 2023
Balisage Paper: Ambiguity in iXML
and how to control it
Norm Tovey-Walsh
Inveterate hacker of markup (XML, HTML, SGML, TeX, JSON,
DocBook, RELAX NG, XML Schema, Schematron) and wrangler of bits
(XProc, XSLT, XQuery, Java, Scala, Python, JavaScript, C#).
Author. Photographer. Occasional cook. Frequent bottle washer.
Employed by Saxonica. Resident of Wales. Website tinkerer,
https://norm.tovey-walsh.com/.
Copyright Norm Tovey-Walsh
Abstract
Humans are really good at resolving ambiguities. Our senses are
trained for it: is that pattern of shadows in the forest dappled
sunlight, or a tiger waiting to pounce? Our minds quickly and almost
effortlessly adjust interpretations based on contextual clues that
change over time. Parsers? Not so much. Our everyday languages and
formats: XML, JSON, JavaScript, Java, etc. are rigorously defined to
avoid ambiguity: you must put a quote here, a semicolon there.
(Most) parsers reject anything that cannot be unambiguously
identified within a small textual window. Invisible XML is an
uncommon format in that it doesn’t reject grammars or parses that
are ambiguous. That doesn’t mean ambiguity is a good thing, and it
doesn’t mean authors wouldn’t like to control it.
Table of Contents
- Introduction
- Terminology
- Backus-Naur forms
-
- Translating EBNF to BNF: an example
- Automated translation of EBNF to BNF
- What is ambiguity?
-
- The parse forest
- “Infinite” ambiguity
- How does ambiguity arise?
- Why does ambiguity arise?
- Resolving ambiguity with priorities
-
- Resolving horizontal ambiguity
- Conclusions
- Appendix A. More complicated algorithmic disambiguation
Introduction
Invisible XML [Hillman et al. 2022a] “is a
method for treating non-XML documents as if they were XML”
[Pemberton 2022]. It is a way of
describing a document such that the underlying, invisible,
structures are exposed, made visible. Invisible XML does this with
a grammar: a set of rules that maps one logical structure onto
another, first mapping the whole document into a few smaller
structures, then mapping each of those structures into smaller
structures, etc. until the mappings are to individual characters.
The processor combines these rules in a way (usually, in all the
possible ways) that matches every character in the document. If
the process succeeds, we say that the document matches the
grammar.
Terminology
The individual characters in a grammar are called “terminals”.
Those are the things you end up with. The only thing that an “a”
in your document can match is a terminal in the grammar that matches an “a”. Higher
level
structures are called “nonterminals”, they can be decomposed
further unto other nonterminals or terminals. Each item in the
grammar, a nonterminal or terminal, is a “symbol”.
A document or other input that matches a grammar is sometimes
called a “sentence” in that grammar. An input that
doesn’t match a grammar is sometimes
described as not being a sentence, but those aren’t very
interesting from the perspective of ambiguity. A non-sentence is
unambigous because it always matches the grammar in exactly zero
ways.
Backus-Naur forms
An Invisible XML grammar is composed of rules.
Each rule is a mapping from a nonterminal on the
left to an expression of nonterminals and terminals on the right.
Grammars described this way are “Backus-Naur forms” or BNF grammars.
There are many different flavors of BNF grammar with different
conventions for how the nonterminals and terminals are identified
and how they can be combined on the right hand sides.
The simplest BNF grammars consist of a nonterminal on the left
hand side and a sequence of symbols on the right:
CAT = 'c', AT
AT = 'a', 't'
That grammar says that the nonterminal CAT matches a terminal
“c” followed by whatever the nonterminal AT matches. The nonterminal
AT matches the terminals “a” followed by “t”. Consequently, this is a
rather boring grammar that matches the word “cat”. Invisible XML
requires that the first rule in the grammar be the starting symbol
when matching an input and that’s the convention used throughout this
paper.
Grammars that allow more complicated expressions on the right hand
side: choices, optionality, repetition, etc. are usually called
Extended Backus-Naur forms or EBNF grammars. Consider:
MAMMAL = ['b' | 'c' | 'r'], AT
AT = 'a', 't'That first rule says that a MAMMAL matches a “b”, “c”, or “r”
followed by AT. The square brackets and vertical bars introduce a
choice, making this an EBNF. Invisible XML is an EBNF grammar, it
allows all sorts of special forms in the expressions on the right
hand side.
Real Talk™: your Invisible XML processor doesn’t parse directly
with Invisible XML, it uses a BNF derived from Invisible XML. (I mean,
it might use Invisible XML directly, but the
author doesn’t know of any processor that does.)
In theoretical computer science, most of the actual parsing
algorithms described are described exclusively in terms of BNF
grammars, and not EBNF grammars. Consequently, the algorithms actually
implemented also work this way. The good news is that any EBNF grammar
can be translated into an equivalent BNF grammar. That’s what the
“Hints for Implementors” section in the Invisible XML specification is
about and that’s why it’s there.
From an authoring perspective, BNF grammars are painfully
restrictive about what can appear on a right hand side. They do
relax one Invisible XML constraint, however, they allow more than
one definition for a nonterminal. Consider the MAMMAL example
above, that can be rewritten in BNF as:
MAMMAL = 'b', AT
MAMMAL = 'c', AT
MAMMAL = 'r', AT
AT = 'a', 't'In short: BNF grammars are simpler to reason about and simpler for
implementations to process. EBNF grammars are easier to author.
All of this translation from EBNF to BNF is relevant for a couple
of reasons.
-
Discussions of ambiguity in computer science literature, like
discussions of parsing in general, tend to be about BNF
grammars.
-
An implementation that exposes its operation to the user is
likely to expose an underlying BNF grammar which may be a bit
disorienting if it’s unexpected.
Translating EBNF to BNF: an example
Consider the following EBNF grammar for an “a” followed by one or more
periods followed by a “b”:
AB = A, '.'*, B.
A = 'a' .
B = 'b' .
To turn that into BNF, we need to replace the extension “*” with
simpler rules. Here’s one possibility:
AB = A, PERIOD_STAR, B
A = 'a'
B = 'b'
PERIOD_STAR = ()
PERIOD_STAR = PERIOD_PLUS
PERIOD_PLUS = '.'
PERIOD_PLUS = '.', PERIOD_PLUSThis says that an ‘a’ can be followed by PERIOD_STAR, followed by
‘b’. The nonterminal PERIOD_STAR can either match nothing at all,
represented as “()” for consistency with iXML, or PERIOD_PLUS.
PERIOD_PLUS can either match a single period or a single period
followed by PERIOD_PLUS. Take a moment to persuade yourself this
grammar does match the same inputs as the Invisible XML version.
Parsing “a..b” with this grammar would produce a tree like this:
<AB>
<A>a</A>
<PERIOD_STAR>
<PERIOD_PLUS>.
<PERIOD_PLUS>.</PERIOD_PLUS>
</PERIOD_PLUS>
</PERIOD_STAR>
<B>b</B>
</AB>
Automated translation of EBNF to BNF
In practice, an Invisible XML processor that translates to BNF
isn’t going to be able to choose simple, obvious names for the
generated nonterminals. Given the original grammar above, when
NineML [Walsh 2022] translates to BNF, it uses the names
$1_L.-star and $2_L.-plus.
Each generated nonterminal begins with $n_. The leading “$” assures
that it won’t clash with nonterminals from the Invisible XML grammar
(because iXML nonterminal symbols can’t contain “$”), “n” is a decimal number that
distinguishes this nonterminal from all the other generated
nonterminals, and what follows the underscore is an attempt to
describe what’s being replaced: in this case a (L)iteral period(.)
star or plus.
What is ambiguity?
Ambiguity occurs when there’s more than one way to match a grammar
to an input. Given an arbitrary grammar, the question “are there
any sentences for which this grammar is ambiguous?” is known to be
undecidable. Here, the focus is on the combination of a grammar
and a particular sentence: “is a parse of this sentence
with this grammar
ambiguous?” Invisible XML processors should be able to answer that
question.
Consider this Invisible XML grammar:
S = A
| B .
A = 'a' .
B = [Ll] .
An input matches S if it matches A or B. An A matches exactly “a”
and B matches any Unicode character in the lowercase letter class (that’s what “[Ll]”
means in iXML;
alternatively you could use a character set such as “['a'-'z']” for unaccented, lowercase
latin letters).
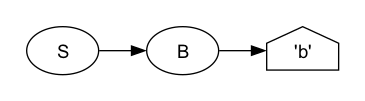
Does this grammar match “b”? Yes it does, unambigously:
<S><B>b</B></S>That’s a very simple tree:
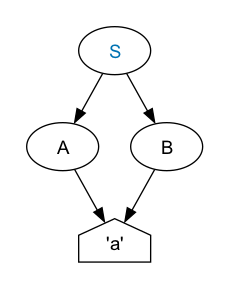
Does it match “a”? Yes, but in two different ways in this case. An
“a” matches both A (a lower case “a”) and B (a lowercase letter).
Consequently either of these outputs is correct:
<S xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<A>a</A></S>or
<S xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<B>a</B></S>We say the result is ambiguous because more than one result is
possible.
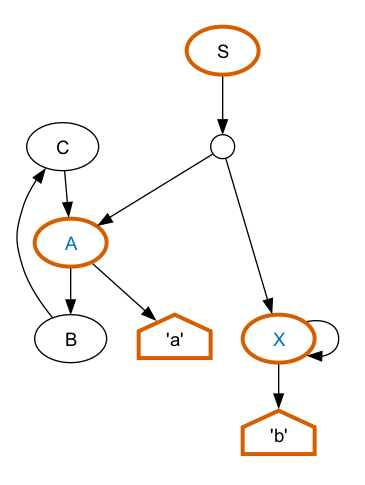
The parse forest
As a practical matter, implementations of Invisible XML have to
be prepared to address ambiguous parses. Many of the algorithms
suitable for this kind of parsing proceed by generating not a
parse tree of the output but a parse forest. Here is a
representation of the parse forest for the grammar above:
The parse forest represents all of the possible parse trees that
can be derived from a particular grammar for a particular input.
The terminal symbols are generally at the bottom of the graph,
shaped like houses, nonterminals above them in ovals.
“Infinite” ambiguity
It is possible for parse forests to contain loops. Consider this
contrived grammar for the sentence “ab”:
S = A, X .
A = "a" | B | () .
B = C .
C = A | () .
X = "b" | X | () .
It matches “ab” but infinitely many times and in infinitely many
ways.
Trivially, you can put as many X elements
around the b as you like. Similarly, you can
go from A to B to
C and back to A as many
times as you like.
Loops like this always involve nonterminals that match “nothing”
because a sequence that consumes a terminal can’t be
infinite. (Unless the input is infinite.)
Grammars can have loops and so an Invisible XML processor has to
do something with them, but they don’t really make a lot of sense in a
grammar designed to produce useful XML output. Infinitely many
<X> tags in a row is going to be hard to parse in a
finite amount of memory and time. Avoid loops. Extracting trees from a
cyclic graph is problematic, and loops don’t have any really coherent
meaning this context.
How does ambiguity arise?
Brabrand, Giegerich, and Møller developed a taxonomy of ambiguity
[Brabrand et al. 2010] and proved
that all ambiguity in a grammar arises in one of two ways:
-
In a choice between two nonterminals that both match part of
the input. They call this “vertical ambiguity”. It arises
from a choice between nonterminals that often appear
vertically aligned with each other in the (BNF) grammar.
-
In a sequence of nonterminals where the end of one subsequence
“overlaps” with the beginning of the next. They call this
“horizontal ambiguity”. It arises in a horizontal sequence of
symbols.
Both of the ambiguous grammars above are examples of vertical
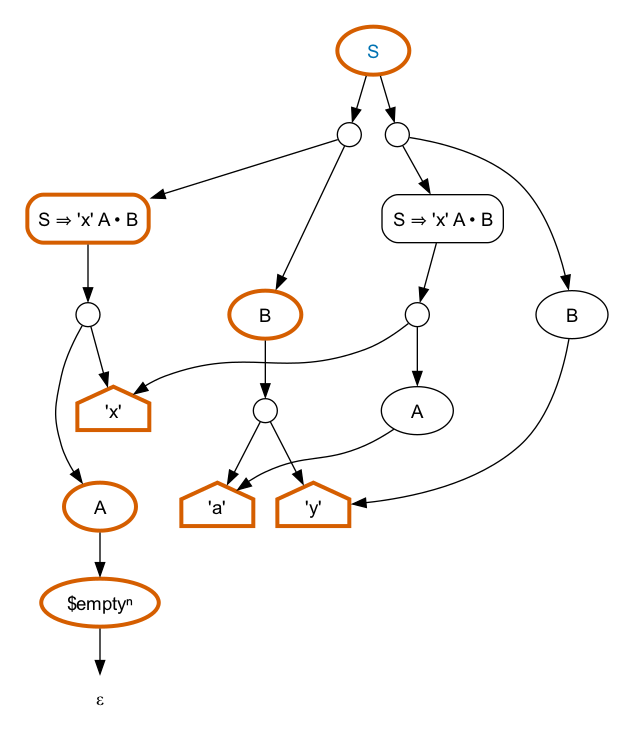
ambiguity. An example of horizontal ambiguity occurs in this
grammar:
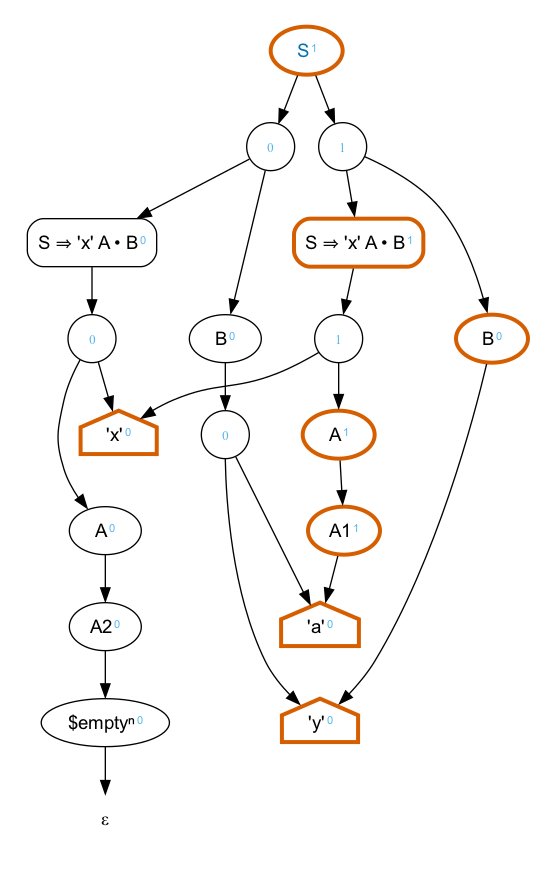
S = "x", A, B .
A = "a" | () .
B = "a", "y" | "y" .
This grammar matches only the input “xay”, but in two different
ways. Either A matches “a” and B matches “y”
or A matches the empty sequence and B matches
“a”, “y”. The parse forest for this example is a little more
complicated.
This graph is not as ambiguous as it might appear at first
glance. There is only one actual ambiguity, from S. Extra nodes
representing intermediate states in the parse (e.g.,
S ⇒ 'x' A • B) have been added to the graph and the graph
has been structured around these nodes. The fact that there are two
edges leading out of the small circular nodes is
not an ambiguity. Those nodes have been added to the graph to make it
binary. This helps to manage the size of the graph, for both memory
and performance reasons, but doesn’t actually effect the inputs
recognized. The choice on the left hand side below S can be understood
as “the symbols that match S ⇒ 'x' A • B, followed by the
symbols that match B”. There isn’t a choice there.
Why does ambiguity arise?
Vertical ambiguity arises when two different nonterminals match
the same input. This often occurs because there are multiple ways
to “match nothing”. Consider this simple grammar for CSS from the
Invisible XML test suite:
css = S, rule+.
rule = selector, block.
block = -"{", S, property**(-";", S), -"}", S.
property = @name, S, -":", S, value | empty.
selector = name, S.
name = letter+.
-letter = ["a"-"z" | "-"].
digit = ["0"-"9"].
value = (@name | @number), S.
number = digit+.
-empty = .
-S = -[" " | #a]*.You might use this grammar for quite a while before noticing that
it’s ambiguous. It’s only ambiguous when the property block is
empty:
$ coffeepot -g:src/css1.ixml "p { }" --no-output
Found 2 possible parses.One way to figure out where the ambiguity arises is to look at all
of the parse trees. The --parse-count option on
CoffeePot will generate more than one parse (note that the output
is not conformant to the specification in this case).
$ coffeepot -g:css1.ixml --parse-count:2 "p { }" --pretty-print
Found 2 possible parses.
<records parses="2" totalParses="2">
<css xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
<rule>
<selector>
<name>p</name>
</selector>
<block/>
</rule>
</css>
<css xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
<rule>
<selector>
<name>p</name>
</selector>
<block>
<property/>
</block>
</rule>
</css>
</records>With a little inspection, you can work out that the difference is
in how the empty block is parsed: is it empty or does it contain
an empty property?
Another way to find the ambiguity is to use the analyzer by Anders
Möller:
$ coffeepot -g:css1.ixml "p { }" --analyze-ambiguity --no-output
The grammar is ambiguous:
*** vertical ambiguity: $2_property-star-sep[#1] <--> $2_property-star-sep[#2]
ambiguous string: ""
Found 2 possible parses.Here we see the ambiguity is vertical and is between two different
ways to match the empty string with
$2_property-star-sep. To get a better
understanding, we can ask for the BNF (lines not relevant to this ambiguity have
been elided for convenience):
$ coffeepot -g:css1.ixml "p { }" --no-output --show-grammar
The Earley grammar (35 rules):
…
4. block ::= '{', S, $2_property-star-sepⁿ, '}', S
5. property ::= name₁, S, ':', S, value
6. property ::= emptyⁿ
…
17. $2_property-star-sepⁿ ::= ε
18. $2_property-star-sepⁿ ::= $3_property-plus-sep
19. $3_property-plus-sep ::= property, $5_L;-starⁿ
…We know the problem is in $2_property-star-sep.
That can be empty or $3_property-plus-sep. And
that can be empty if
property is empty. There’s our ambiguity.
(Note that the NineML output uses ε rather than “()” to represent “matches nothing”.
That’s
another common convention.)
The fix is easy, given that block can contain
zero or more property matches, there’s no
reason to allow property itself to be empty.
This grammar is unambiguous:
css = S, rule+.
rule = selector, block.
block = -"{", S, property**(-";", S), -"}", S.
property = @name, S, -":", S, value .
selector = name, S.
name = letter+.
-letter = ["a"-"z" | "-"].
digit = ["0"-"9"].
value = (@name | @number), S.
number = digit+.
-S = -[" " | #a]*.Horizontal ambiguity arises when there are multiple ways to match
a sequence of tokens in a rule. Here’s a simple grammar for North
American phone numbers (555-1212, +1-512-555-1212, 5551212, etc.):
phone-number = cc, incountry .
cc = "+1", sep | +"+1" .
-incountry = (areacode, sep)?, prefix, sep, number .
-sep = dash | space .
-dash = -'-'? .
-space = -' '? .
number = digits .
prefix = digits .
areacode = digits | -'(', digits, -')' .
-digits = ['0'-'9']+ .At first glance, it works fine. Parsing “555-555-1212” produces:
<phone-number>
<cc>+1</cc>
<areacode>555</areacode>
<prefix>555</prefix>
<number>1212</number>
</phone-number>
Parsing “5551212” however…finds 72 possible parses! The ambiguity
analyzer really helps here:
The grammar is ambiguous:
*** vertical ambiguity: sep[#1] <--> sep[#2]
ambiguous string: ""
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] <--> prefix[prefix] sep[sep] number[number]
ambiguous string: "000"
matched as "" <--> "000" or "0" <--> "00"
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] prefix[prefix] <--> sep[sep] number[number]
ambiguous string: "000"
matched as "0" <--> "00" or "00" <--> "0"
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] prefix[prefix] sep[sep] <--> number[number]
ambiguous string: "000"
matched as "0" <--> "00" or "00" <--> "0"
This reveals all sorts of ways to match area codes, prefixes,
and numbers. The grammar unrealistically allows any number of digits
in those nonterminals. So “5551212” can be divided into three sections
at arbitrary locations. In reality, area codes and prefixes are always
three digits and numbers are always four. This grammar:
phone-number = cc, incountry .
cc = "+1", sep | +"+1" .
-incountry = (areacode, sep)?, prefix, sep, number .
-sep = dash | space .
-dash = -'-'? .
-space = -' '? .
number = digits4 .
prefix = digits3 .
areacode = digits3 | -'(', digits3, -')' .
-digits3 = digit, digit, digit .
-digits4 = digits3, digit .
-digit = ['0'-'9'] .Does better:
coffeepot -g:phone2.ixml 5551212 -pp --analyze-ambiguity
The grammar is ambiguous:
*** vertical ambiguity: sep[#1] <--> sep[#2]
ambiguous string: ""
Found 2 possible parses.
<phone-number xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<cc>+1</cc>
<prefix>555</prefix>
<number>1212</number>
</phone-number>
There’s still a vertical ambiguity which we’ll leave as an
exercise for the reader. It can easily be removed and the analyzer is
focusing your attention on “sep”.
Sometimes ambiguity arises because the data is inherently
ambiguous. Consider a project with due dates. If you have
collaborators on both sides of the Atlantic, you may get dates in
a variety of formats: the “US style”: mm/dd/yyyy, the “European
style”: dd/mm/yyyy, or the
“correct style”:
yyyy-mm-dd. A grammar for due dates might look like this:
deadline = -'due', -' '+, date .
date = usdate | eudate | isodate .
-usdate = month, -'/', day, -'/', year .
-eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
month = d, d? .
day = d, d? .
year = d, d, d, d .
-d = ['0'-'9'] .In this grammar, parsing “due 7/31/2023” is (vertically) ambiguous. Such a date matches
either a US date:
<deadline xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<date>
<month>7</month>
<day>31</day>
<year>2023</year>
</date>
</deadline>or an EU date:
<deadline xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<date>
<day>7</day>
<month>31</month>
<year>2023</year>
</date>
</deadline>Wait. What? The EU date is absurd. We can easily improve this grammar by
observing that not all two digit numbers are valid months and
days:
deadline = -'due', -' '+, date .
date = usdate | eudate | isodate .
-usdate = month, -'/', day, -'/', year .
-eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
month = '0'?, d | '10' | '11' | '12' .
day = ['0'-'2']?, d | '30' | '31' .
year = d, d, d, d .
-d = ['0'-'9'] .Now 7/31/2023 is no longer ambiguous, but 8/1/2023 is
still ambiguous.
If it’s possible to change the data to remove the ambiguity, for
example by using “.” as separator in EU style dates instead of
“/”, then the ambiguity will go away. If that’s not possible,
there is always going to be ambiguity in the parsing because the
data is inherently ambiguous.
Ambiguity can also arise in grammars for data that isn’t
inherently ambiguous. Consider the following contrived example for
a sequence of “a”s separated by optional periods or a sequence of
“b”s separated by optional periods:
list = list-of-a | list-of-b .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
A = 'a' .
B = 'b' .
-s = -['.']* .This will happily, and unambigously, parse a list of “a” or a list
of “b”, for example: “a..a.aa”:
<list><A>a</A><A>a</A><A>a</A><A>a</A></list>(In a more familiar example of this kind of grammar,
s would be whitespace, for example,
-[' ' | #a | #d | #9]*. A period is used as a
separator in these examples only because it’s easier to see in the
output.)
Suppose you want instead to parse a list of “a”, or a list of “b”,
or a list of “a” followed by a list of “b”, all separated by
optional periods. For example “a.a.bb”. This seems easy. A list
becomes an optional list-of-a followed by an
optional list-of-b possibly separated by
periods:
list = list-of-a?, s, list-of-b? .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
A = 'a' .
B = 'b' .
-s = -['.']* .Unfortunately, this is ambiguous. There are two possible parses:
$ coffeepot -g:list-ab.ixml a.a.bb --parse-count:all
Found 2 possible parses.
<records parses="2" totalParses="2">
<list xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
<A>a</A><A>a</A><B>b</B><B>b</B>
</list>
<list xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
<A>a</A><A>a</A><B>b</B><B>b</B>
</list>
</records>
There are two possible parses, but they’re both the
same!
Because “-” is used to elide parts of the input in Invisible XML,
it’s easy to forget that those elided parts are still in the
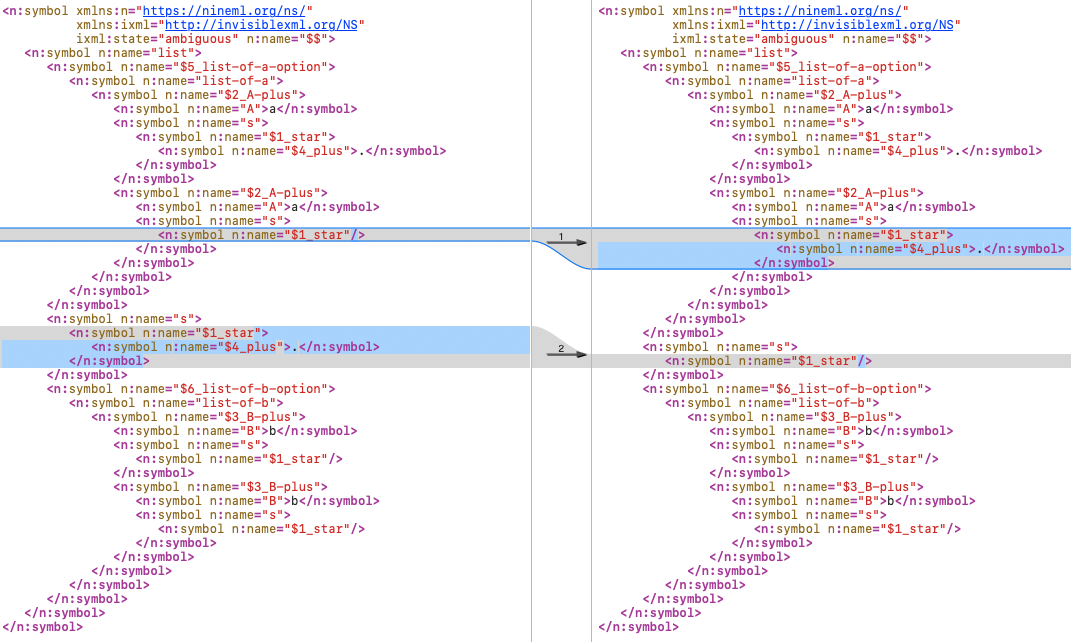
parsed result. If we look at a full parse trees, including all of
the generated nonterminals and marks, the difference becomes
visible.
The difference is whether the “.” is consumed by the “s” in the
list-of-a nonterminal or the “s” between the
lists. This is horizontal ambiguity. It’s also visible in the
parse forest, although the forest is getting rather large at this
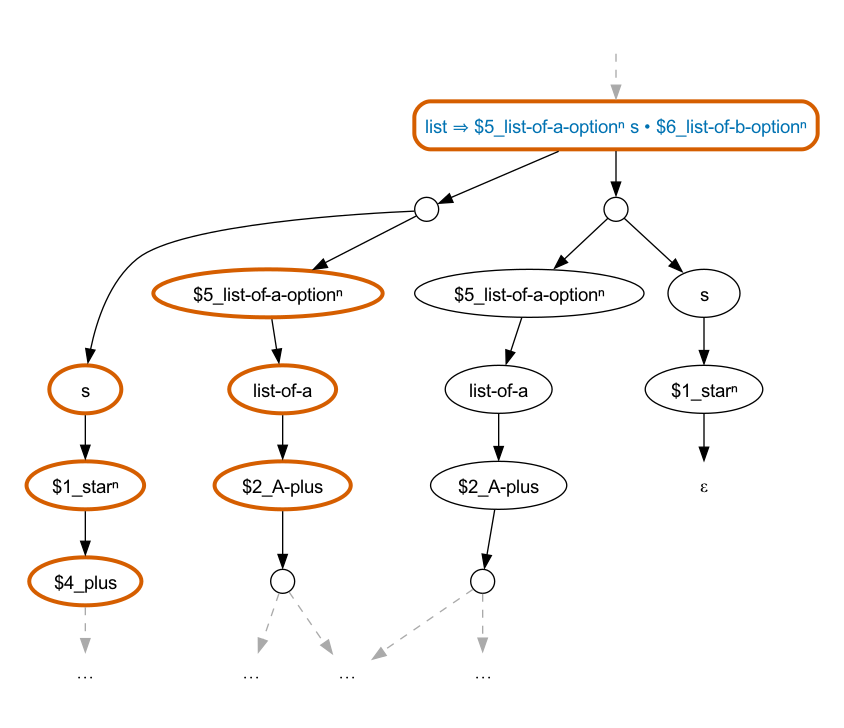
point. Looking at just a portion of the forest, we see:
Here, the selected parse consumes the “.” in the
list-of-a nonterminal, leaving the
s between the lists matching the empty
sequence. (The diagrams are generated with GraphViz and it’s worth observing
that the order of the nodes in the diagram doesn’t always reflect the order in the
input; here
the selected “s” is visually on the left although in fact it occurs after
the “$5_list-of-a-option”.)
If the input data is unambiguous, it is always in principle
possible to write the grammar such that it is unambiguous. There
are a couple of options in this grammar. Perhaps the easiest is
simply to remove the s between the lists:
list = list-of-a?, list-of-b? .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
A = 'a' .
B = 'b' .
-s = -['.']* .Any periods between the last “a” and the first “b” will be
consumed by the s after the A. They are elided
in the output so it makes no difference how they are consumed.
Alternatively, the lists can be rewritten so that they don’t end
with s, then the s between
the lists is unambiguous:
list = list-of-a?, s, list-of-b? .
-list-of-a = ((A, s)*, A)? .
-list-of-b = ((B, s)*, B)? .
A = 'a' .
B = 'b' .
-s = -['.']* .When designing grammars with optional separators, especially, for
example, whitespace, it is good practices to do either one of two
things:
-
Put all optional separators at the end of nonterminals.
-
Put all optional separators between nonterminals (and not at
the ends).
But do not do both.
Resolving ambiguity with priorities
If your grammar can be made unambiguous, make it unambiguous. An
unambiguous parse can be performed faster and will use less
memory. All Invisible XML processors will produce the same results
for an unambiguous parse.
If your grammar can be made unambiguous, make it unambiguous!
In an effort to address those cases where it can’t, where either
the data is inherently unambiguous or the complexity of the
grammar conspires to make it hard to disambiguate, the NineML
suite of tools introduce an extension to Invisible XML: the
ability to assign priorities to nonterminals.
Consider again the grammar for US, European, and ISO 8601 dates.
Suppose you know that the overwhelming majority of your data is
from the United States. You might decide that whenever a date is
ambiguous, it’s a US date: that 8/1/2023 is the first of August,
not the eighth of January. You want to make the
usdate nonterminal “higher priority” than the
eudate nonterminal.
NineML uses pragmas to assign priorities. Pragmas were introduced
at Balisage 2022 in [Hillman et al. 2022b].
Pragmas are delimited with {[ and
]}, so they appear as comments to a
pragma-unaware processor.
{[+pragma n "https://nineml.org/ns/pragma/"]}
deadline = -'due', -' '+, date .
date = usdate | eudate | isodate .
{[n priority 2]} -usdate = month, -'/', day, -'/', year .
-eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
month = '0'?, d | '10' | '11' | '12' .
day = ['0'-'2']?, d | '30' | '31' .
year = d, d, d, d .
-d = ['0'-'9'] .The declaration at the top of the file, is a pragma that
associates n with a URI. The NineML family of
tools recognize that URI, so the subsequent n
pragma is interpreted as a priority. (If a different URI had been
used to define n, NineML would simply have
ignored the pragma as unrecognized.)
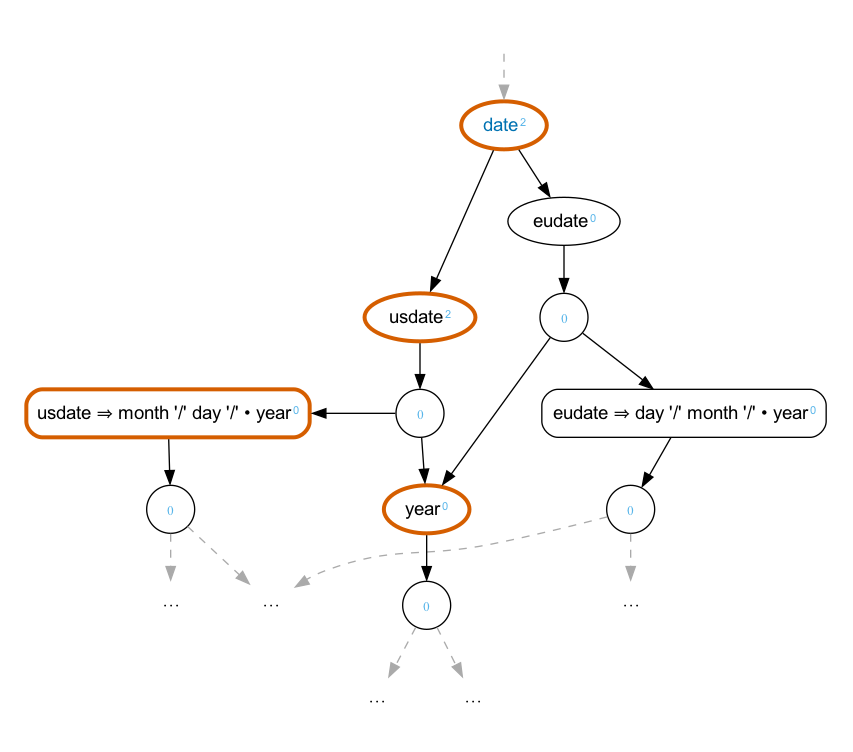
In the resulting parse forest, priorities accumulate “up” the
graph. At any point where a choice must be made, if one branch has
a larger priority than all of the others, it will always be
selected. Here is a portion of the parse forest for “1/8/2023”
with this grammar:
NineML will always favor the usdate over the
eudate because it has the higher priority.
There are two ways to accumulate priorities. By default, the
priority of any node is equal to the highest priority among the
nodes below it. Alternatively, the priority can be the sum of all
of the priorities below it.
This can be used to achieve some interesting effects. Consider
this grammar:
{[+pragma n "https://nineml.org/ns/pragma/"]}
deadline = -'due', -' '+, date .
date = usdate | eudate | isodate .
{[n priority 4]} -usdate = month, -'/', day, -'/', anyyear .
{[n priority 3]} -eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
month = '0'?, d | '10' | '11' | '12' .
day = ['0'-'2']?, d | '30' | '31' .
anyyear = d, d, d, d .
year = newer | older .
{[n priority 2]} -newer = '2', d, d, d .
-older = '1', d, d, d .
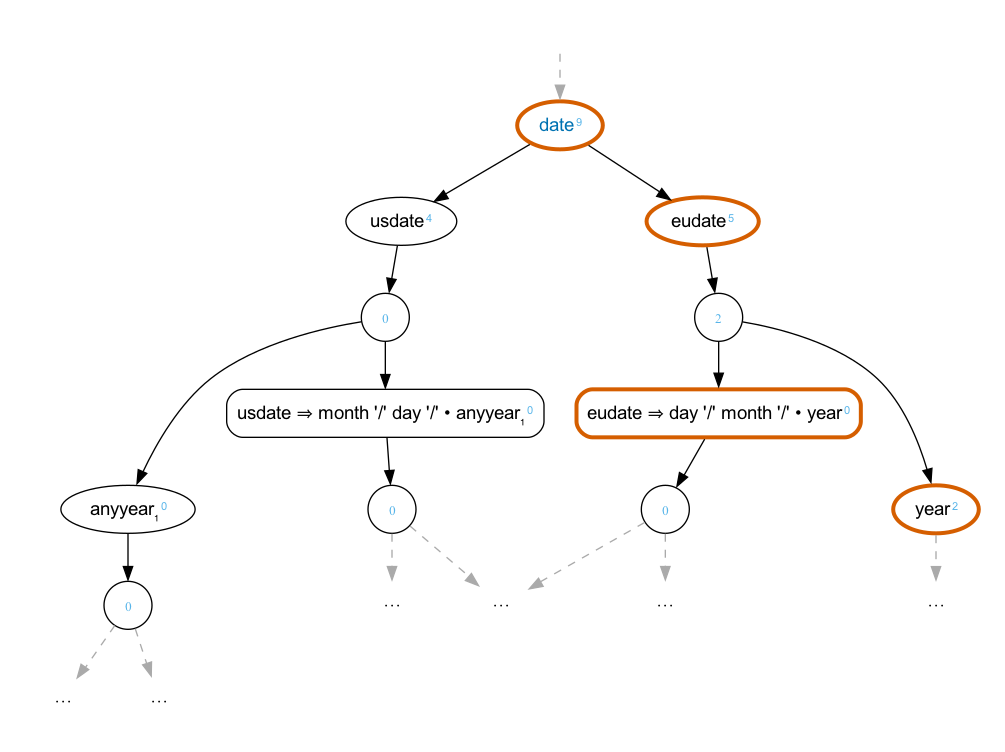
-d = ['0'-'9'] .Using the default accumulation strategy, the
usdate will always be preferred. However, if
the summing strategy is used, eudates will be
preferred for years 2000 and beyond:
It’s critical to observe that priorities in NineML are used when
selecting a tree from the parse forest. They have no
effect on the parsing. It might be possible to change
the actual parsing algorithms to take account of priorities, but
that’s not what NineML does.
Resolving horizontal ambiguity
Applying priorities does not immediately give us a mechanism for
resolving horizontal ambiguity because there’s nowhere to hang
the priorities. The ambiguity in the earlier “xay” example is
between two of the intermediate states. Neither a priority on A
nor a priority on B will resolve it.
We can, however, introduce new nonterminals to turn the
horizontal ambiguity into vertical ambiguity. Consider:
{[+pragma n "https://nineml.org/ns/pragma/"]}
S = "x", A, B .
A = A1 | A2 .
{[n priority 1]} -A1 = "a" .
-A2 = () .
B = "a", "y" | "y" .In this grammar, the alternative that favors A matching “a” will
always be selected.
Moving the higher priority to A2 would have
the opposite effect. A similar transformation applied to B
would also disambiguate the alternatives.
Conclusions
-
Ambiguity is a fact of life. In BNF grammars, all ambiguities are either horizontal
or vertical. Tools exist which can (usually) identify the kind of grammatical ambiguity
present in a grammar and suggest inputs which will exercise it.
-
Many ambiguities arise where there are different alternatives that can “match nothing.”
Optional whitespace is a common example. As a rule of thumb, where optional separators
can occur,
place them at the ends of symbols, or between symbols, but not both.
-
Ambiguity is bad. If your grammar can be
made unambiguous, make it unambiguous!
-
If your grammar can’t be made unambiguous, it may be possible guide the parser
into selecting the trees that you prefer.
Appendix A. More complicated algorithmic disambiguation
NineML also allows you to make choices with XPath expressions or
with an XSLT or XQuery function. Using XSLT or XQuery, you can make
arbitrary choices, including ones which traverse loops.
The function receives the input string, a description of the
parse forest, and a description of the choice to be made. It is free to make
any choice it wishes and record details for use in subsequent choices.
As an illustrative example, when parsing dates with the grammar above,
the following function will select European dates on years
evenly divisible by five and US dates otherwise:
<xsl:function name="cp:choose-alternative" as="map(*)">
<xsl:param name="context" as="element()"/>
<xsl:param name="options" as="map(*)"/>
<xsl:variable name="year"
select="substring($options?input, $context/@start + $context/@length - 4)"/>
<xsl:variable name="selection" as="xs:string">
<xsl:choose>
<xsl:when test="xs:integer($year) mod 5 = 0">
<xsl:sequence select="$context/children[symbol[@name='eudate']]/@id/string()"/>
</xsl:when>
<xsl:otherwise>
<xsl:sequence select="$context/children[symbol[@name='usdate']]/@id/string()"/>
</xsl:otherwise>
</xsl:choose>
</xsl:variable>
<xsl:sequence select="map { 'selection': $selection }"/>
</xsl:function>A situation in which that was a sensible choice is a little hard
to imagine, but it suffices as an example. For more details, see the
CoffeePot documentation.
References
[Brabrand et al. 2010] Brabrand, Claus, Robert
Giegerich, and Anders Möller. “Analyzing Ambiguity of Context-Free Grammars.”
Science of Computer Programming, volume 75, number 3.
Elsevier. (2010).
https://cs.au.dk/~amoeller/papers/ambiguity/. doi:https://doi.org/10.1016/j.scico.2009.11.002.
[Hillman et al. 2022a] Hillman, Tomos, John Lumley,
Steven Pemberton, C. M. Sperberg-McQueen, Bethan Tovey-Walsh and Norm
Tovey-Walsh. “Invisible XML coming into focus: Status report from the
community group.” Presented at Balisage: The Markup Conference 2022,
Washington, DC, August 1 - 5, 2022. In Proceedings of Balisage: The
Markup Conference 2022. Balisage Series on Markup Technologies, vol.
27 (2022). doi:https://doi.org/10.4242/BalisageVol27.Eccl01.
[Hillman et al. 2022b] Hillman, Tomos, C. M.
Sperberg-McQueen, Bethan Tovey-Walsh and Norm Tovey-Walsh. “Designing
for change: Pragmas in Invisible XML as an extensibility mechanism.”
Presented at Balisage: The Markup Conference 2022, Washington, DC,
August 1 - 5, 2022. In Proceedings of Balisage: The Markup
Conference 2022. Balisage Series on Markup Technologies, vol. 27
(2022). doi:https://doi.org/10.4242/BalisageVol27.Sperberg-McQueen01.
[Pemberton 2022] Pemberton, Steven. “Invisible
XML Specification.” Published by the Invisible Markup Community Group
on the web at https://invisiblexml.org/1.0/.
[Walsh 2022] NineML: a family of Invisible XML tools.
https://nineml.org/.
×Hillman, Tomos, John Lumley,
Steven Pemberton, C. M. Sperberg-McQueen, Bethan Tovey-Walsh and Norm
Tovey-Walsh. “Invisible XML coming into focus: Status report from the
community group.” Presented at Balisage: The Markup Conference 2022,
Washington, DC, August 1 - 5, 2022. In Proceedings of Balisage: The
Markup Conference 2022. Balisage Series on Markup Technologies, vol.
27 (2022). doi:https://doi.org/10.4242/BalisageVol27.Eccl01.
×Hillman, Tomos, C. M.
Sperberg-McQueen, Bethan Tovey-Walsh and Norm Tovey-Walsh. “Designing
for change: Pragmas in Invisible XML as an extensibility mechanism.”
Presented at Balisage: The Markup Conference 2022, Washington, DC,
August 1 - 5, 2022. In Proceedings of Balisage: The Markup
Conference 2022. Balisage Series on Markup Technologies, vol. 27
(2022). doi:https://doi.org/10.4242/BalisageVol27.Sperberg-McQueen01.