Balisage Paper: Ambiguity in iXML

Introduction

Invisible XML [Hillman et al. 2022a] “is a method for treating non-XML documents as if they were XML” [Pemberton 2022]. It is a way of describing a document such that the underlying, invisible, structures are exposed, made visible. Invisible XML does this with a grammar: a set of rules that maps one logical structure onto another, first mapping the whole document into a few smaller structures, then mapping each of those structures into smaller structures, etc. until the mappings are to individual characters. The processor combines these rules in a way (usually, in all the possible ways) that matches every character in the document. If the process succeeds, we say that the document matches the grammar.

Terminology

The individual characters in a grammar are called “terminals”. Those are the things you end up with. The only thing that an “a” in your document can match is a terminal in the grammar that matches an “a”. Higher level structures are called “nonterminals”, they can be decomposed further unto other nonterminals or terminals. Each item in the grammar, a nonterminal or terminal, is a “symbol”.

A document or other input that matches a grammar is sometimes called a “sentence” in that grammar. An input that doesn’t match a grammar is sometimes described as not being a sentence, but those aren’t very interesting from the perspective of ambiguity. A non-sentence is unambigous because it always matches the grammar in exactly zero ways.

Backus-Naur forms

An Invisible XML grammar is composed of rules. Each rule is a mapping from a nonterminal on the left to an expression of nonterminals and terminals on the right. Grammars described this way are “Backus-Naur forms” or BNF grammars. There are many different flavors of BNF grammar with different conventions for how the nonterminals and terminals are identified and how they can be combined on the right hand sides.

The simplest BNF grammars consist of a nonterminal on the left hand side and a sequence of symbols on the right:

CAT = 'c', AT
 AT = 'a', 't'

That grammar says that the nonterminal CAT matches a terminal “c” followed by whatever the nonterminal AT matches. The nonterminal AT matches the terminals “a” followed by “t”. Consequently, this is a rather boring grammar that matches the word “cat”. Invisible XML requires that the first rule in the grammar be the starting symbol when matching an input and that’s the convention used throughout this paper.

Grammars that allow more complicated expressions on the right hand side: choices, optionality, repetition, etc. are usually called Extended Backus-Naur forms or EBNF grammars. Consider:

MAMMAL = ['b' | 'c' | 'r'], AT
    AT = 'a', 't'

That first rule says that a MAMMAL matches a “b”, “c”, or “r” followed by AT. The square brackets and vertical bars introduce a choice, making this an EBNF. Invisible XML is an EBNF grammar, it allows all sorts of special forms in the expressions on the right hand side.

Real Talk™: your Invisible XML processor doesn’t parse directly with Invisible XML, it uses a BNF derived from Invisible XML. (I mean, it might use Invisible XML directly, but the author doesn’t know of any processor that does.)

In theoretical computer science, most of the actual parsing algorithms described are described exclusively in terms of BNF grammars, and not EBNF grammars. Consequently, the algorithms actually implemented also work this way. The good news is that any EBNF grammar can be translated into an equivalent BNF grammar. That’s what the “Hints for Implementors” section in the Invisible XML specification is about and that’s why it’s there.

From an authoring perspective, BNF grammars are painfully restrictive about what can appear on a right hand side. They do relax one Invisible XML constraint, however, they allow more than one definition for a nonterminal. Consider the MAMMAL example above, that can be rewritten in BNF as:

MAMMAL = 'b', AT
MAMMAL = 'c', AT
MAMMAL = 'r', AT
    AT = 'a', 't'

In short: BNF grammars are simpler to reason about and simpler for implementations to process. EBNF grammars are easier to author.

All of this translation from EBNF to BNF is relevant for a couple of reasons.

AB = A, '.'*, B.
 A = 'a' .
 B = 'b' .

         AB = A, PERIOD_STAR, B
          A = 'a'
          B = 'b'
PERIOD_STAR = ()
PERIOD_STAR = PERIOD_PLUS
PERIOD_PLUS = '.'
PERIOD_PLUS = '.', PERIOD_PLUS

                     
<AB>
<A>a</A>
<PERIOD_STAR>
<PERIOD_PLUS>.
<PERIOD_PLUS>.</PERIOD_PLUS>
</PERIOD_PLUS>
</PERIOD_STAR>
<B>b</B>
</AB>

What is ambiguity?

Ambiguity occurs when there’s more than one way to match a grammar to an input. Given an arbitrary grammar, the question “are there any sentences for which this grammar is ambiguous?” is known to be undecidable. Here, the focus is on the combination of a grammar and a particular sentence: “is a parse of this sentence with this grammar ambiguous?” Invisible XML processors should be able to answer that question.

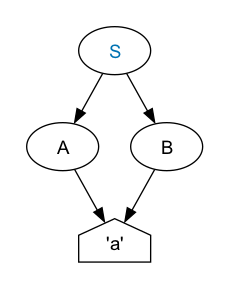
Consider this Invisible XML grammar:

S = A
  | B .
A = 'a' .
B = [Ll] .

An input matches S if it matches A or B. An A matches exactly “a” and B matches any Unicode character in the lowercase letter class (that’s what “[Ll]” means in iXML; alternatively you could use a character set such as “['a'-'z']” for unaccented, lowercase latin letters). Does this grammar match “b”? Yes it does, unambigously:

                  
<S><B>b</B></S>

That’s a very simple tree:

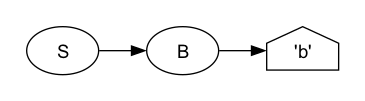
Does it match “a”? Yes, but in two different ways in this case. An “a” matches both A (a lower case “a”) and B (a lowercase letter). Consequently either of these outputs is correct:

                  
<S xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<A>a</A></S>

or

                  
<S xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
<B>a</B></S>

We say the result is ambiguous because more than one result is possible.

The parse forest

As a practical matter, implementations of Invisible XML have to be prepared to address ambiguous parses. Many of the algorithms suitable for this kind of parsing proceed by generating not a parse tree of the output but a parse forest. Here is a representation of the parse forest for the grammar above:

The parse forest represents all of the possible parse trees that can be derived from a particular grammar for a particular input. The terminal symbols are generally at the bottom of the graph, shaped like houses, nonterminals above them in ovals.

“Infinite” ambiguity

It is possible for parse forests to contain loops. Consider this contrived grammar for the sentence “ab”:

S = A, X .
A = "a" | B | () .
B = C .
C = A | () .
X = "b" | X | () .

It matches “ab” but infinitely many times and in infinitely many ways.

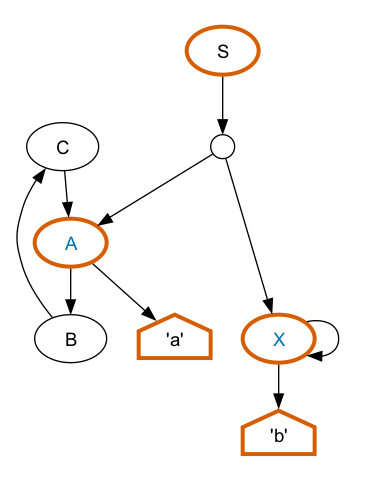
Trivially, you can put as many X elements around the b as you like. Similarly, you can go from A to B to C and back to A as many times as you like. Loops like this always involve nonterminals that match “nothing” because a sequence that consumes a terminal can’t be infinite. (Unless the input is infinite.)

Grammars can have loops and so an Invisible XML processor has to do something with them, but they don’t really make a lot of sense in a grammar designed to produce useful XML output. Infinitely many <X> tags in a row is going to be hard to parse in a finite amount of memory and time. Avoid loops. Extracting trees from a cyclic graph is problematic, and loops don’t have any really coherent meaning this context.

How does ambiguity arise?

Brabrand, Giegerich, and Møller developed a taxonomy of ambiguity [Brabrand et al. 2010] and proved that all ambiguity in a grammar arises in one of two ways:

Both of the ambiguous grammars above are examples of vertical ambiguity. An example of horizontal ambiguity occurs in this grammar:

S = "x", A, B .
A = "a" | () .
B = "a", "y" | "y" .

This grammar matches only the input “xay”, but in two different ways. Either A matches “a” and B matches “y” or A matches the empty sequence and B matches “a”, “y”. The parse forest for this example is a little more complicated.

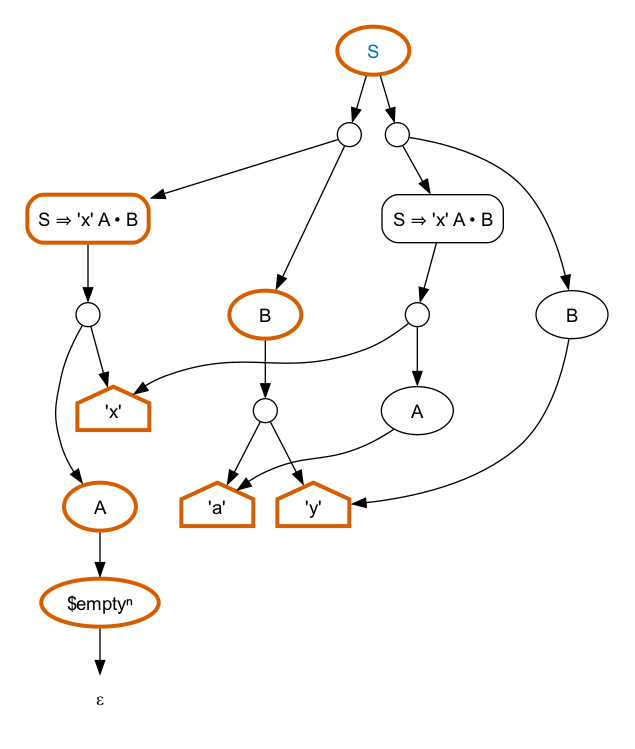
This graph is not as ambiguous as it might appear at first glance. There is only one actual ambiguity, from S. Extra nodes representing intermediate states in the parse (e.g., S ⇒ 'x' A • B) have been added to the graph and the graph has been structured around these nodes. The fact that there are two edges leading out of the small circular nodes is not an ambiguity. Those nodes have been added to the graph to make it binary. This helps to manage the size of the graph, for both memory and performance reasons, but doesn’t actually effect the inputs recognized. The choice on the left hand side below S can be understood as “the symbols that match S ⇒ 'x' A • B, followed by the symbols that match B”. There isn’t a choice there.

Why does ambiguity arise?

Vertical ambiguity arises when two different nonterminals match the same input. This often occurs because there are multiple ways to “match nothing”. Consider this simple grammar for CSS from the Invisible XML test suite:

                  
     css = S, rule+.
    rule = selector, block.
   block = -"{", S, property**(-";", S), -"}", S.
property =  @name, S, -":", S, value | empty.
selector = name, S.
    name = letter+.
 -letter = ["a"-"z" | "-"].
   digit = ["0"-"9"].
   value = (@name | @number), S.
  number = digit+.
  -empty = .
      -S = -[" " | #a]*.

You might use this grammar for quite a while before noticing that it’s ambiguous. It’s only ambiguous when the property block is empty:

$ coffeepot -g:src/css1.ixml "p { }" --no-output
Found 2 possible parses.

One way to figure out where the ambiguity arises is to look at all of the parse trees. The --parse-count option on CoffeePot will generate more than one parse (note that the output is not conformant to the specification in this case).

$ coffeepot -g:css1.ixml --parse-count:2 "p { }" --pretty-print
Found 2 possible parses.
<records parses="2" totalParses="2">
<css xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
   <rule>
      <selector>
         <name>p</name>
      </selector>
      <block/>
   </rule>
</css>
<css xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
   <rule>
      <selector>
         <name>p</name>
      </selector>
      <block>
         <property/>
      </block>
   </rule>
</css>
</records>

With a little inspection, you can work out that the difference is in how the empty block is parsed: is it empty or does it contain an empty property?

Another way to find the ambiguity is to use the analyzer by Anders Möller:

$ coffeepot -g:css1.ixml "p { }" --analyze-ambiguity --no-output
The grammar is ambiguous:
*** vertical ambiguity: $2_property-star-sep[#1] <--> $2_property-star-sep[#2]
ambiguous string: ""

Found 2 possible parses.

Here we see the ambiguity is vertical and is between two different ways to match the empty string with $2_property-star-sep. To get a better understanding, we can ask for the BNF (lines not relevant to this ambiguity have been elided for convenience):

$ coffeepot -g:css1.ixml "p { }" --no-output --show-grammar
The Earley grammar (35 rules):
…
4.                 block ::= '{', S, $2_property-star-sepⁿ, '}', S
5.              property ::= name₁, S, ':', S, value
6.              property ::= emptyⁿ
…
17. $2_property-star-sepⁿ ::= ε
18. $2_property-star-sepⁿ ::= $3_property-plus-sep
19.  $3_property-plus-sep ::= property, $5_L;-starⁿ
…

We know the problem is in $2_property-star-sep. That can be empty or $3_property-plus-sep. And that can be empty if property is empty. There’s our ambiguity. (Note that the NineML output uses ε rather than “()” to represent “matches nothing”. That’s another common convention.)

The fix is easy, given that block can contain zero or more property matches, there’s no reason to allow property itself to be empty. This grammar is unambiguous:

                  
     css = S, rule+.
    rule = selector, block.
   block = -"{", S, property**(-";", S), -"}", S.
property =  @name, S, -":", S, value .
selector = name, S.
    name = letter+.
 -letter = ["a"-"z" | "-"].
   digit = ["0"-"9"].
   value = (@name | @number), S.
  number = digit+.
      -S = -[" " | #a]*.

Horizontal ambiguity arises when there are multiple ways to match a sequence of tokens in a rule. Here’s a simple grammar for North American phone numbers (555-1212, +1-512-555-1212, 5551212, etc.):

phone-number = cc, incountry .
          cc = "+1", sep | +"+1" .
  -incountry = (areacode, sep)?, prefix, sep, number .
        -sep = dash | space .
       -dash = -'-'? .
      -space = -' '? .
      number = digits .
      prefix = digits .
    areacode = digits | -'(', digits, -')' .
     -digits = ['0'-'9']+ .

At first glance, it works fine. Parsing “555-555-1212” produces:

<phone-number>
  <cc>+1</cc>
  <areacode>555</areacode>
  <prefix>555</prefix>
  <number>1212</number>
</phone-number>

Parsing “5551212” however…finds 72 possible parses! The ambiguity analyzer really helps here:

The grammar is ambiguous:
*** vertical ambiguity: sep[#1] <--> sep[#2]
ambiguous string: ""
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] <--> prefix[prefix] sep[sep] number[number]
ambiguous string: "000"
matched as "" <--> "000" or "0" <--> "00"
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] prefix[prefix] <--> sep[sep] number[number]
ambiguous string: "000"
matched as "0" <--> "00" or "00" <--> "0"
*** horizontal ambiguity: incountry[#1]: $2_areacode-option[$2_areacode-option] prefix[prefix] sep[sep] <--> number[number]
ambiguous string: "000"
matched as "0" <--> "00" or "00" <--> "0"

This reveals all sorts of ways to match area codes, prefixes, and numbers. The grammar unrealistically allows any number of digits in those nonterminals. So “5551212” can be divided into three sections at arbitrary locations. In reality, area codes and prefixes are always three digits and numbers are always four. This grammar:

phone-number = cc, incountry .
          cc = "+1", sep | +"+1" .
  -incountry = (areacode, sep)?, prefix, sep, number .
        -sep = dash | space .
       -dash = -'-'? .
      -space = -' '? .
      number = digits4 .
      prefix = digits3 .
    areacode = digits3 | -'(', digits3, -')' .
    -digits3 = digit, digit, digit .
    -digits4 = digits3, digit .
      -digit = ['0'-'9'] .

Does better:

coffeepot -g:phone2.ixml 5551212 -pp --analyze-ambiguity
The grammar is ambiguous:
*** vertical ambiguity: sep[#1] <--> sep[#2]
ambiguous string: ""

Found 2 possible parses.
<phone-number xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
  <cc>+1</cc>
  <prefix>555</prefix>
  <number>1212</number>
</phone-number>

There’s still a vertical ambiguity which we’ll leave as an exercise for the reader. It can easily be removed and the analyzer is focusing your attention on “sep”.

Sometimes ambiguity arises because the data is inherently ambiguous. Consider a project with due dates. If you have collaborators on both sides of the Atlantic, you may get dates in a variety of formats: the “US style”: mm/dd/yyyy, the “European style”: dd/mm/yyyy, or the “correct style”: yyyy-mm-dd. A grammar for due dates might look like this:

deadline = -'due', -' '+, date .
    date = usdate | eudate | isodate .
 -usdate = month, -'/', day, -'/', year .
 -eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
   month = d, d? .
     day = d, d? .
    year = d, d, d, d .
      -d = ['0'-'9'] .

In this grammar, parsing “due 7/31/2023” is (vertically) ambiguous. Such a date matches either a US date:

                  
<deadline xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
  <date>
    <month>7</month>
    <day>31</day>
    <year>2023</year>
  </date>
</deadline>

or an EU date:

                  
<deadline xmlns:ixml="http://invisiblexml.org/NS" ixml:state="ambiguous">
  <date>
    <day>7</day>
    <month>31</month>
   <year>2023</year>
  </date>
</deadline>

Wait. What? The EU date is absurd. We can easily improve this grammar by observing that not all two digit numbers are valid months and days:

deadline = -'due', -' '+, date .
    date = usdate | eudate | isodate .
 -usdate = month, -'/', day, -'/', year .
 -eudate = day, -'/', month, -'/', year .
-isodate = year, -'-', month, -'-', day .
   month = '0'?, d | '10' | '11' | '12' .
     day = ['0'-'2']?, d | '30' | '31' .
    year = d, d, d, d .
      -d = ['0'-'9'] .

Now 7/31/2023 is no longer ambiguous, but 8/1/2023 is still ambiguous.

If it’s possible to change the data to remove the ambiguity, for example by using “.” as separator in EU style dates instead of “/”, then the ambiguity will go away. If that’s not possible, there is always going to be ambiguity in the parsing because the data is inherently ambiguous.

Ambiguity can also arise in grammars for data that isn’t inherently ambiguous. Consider the following contrived example for a sequence of “a”s separated by optional periods or a sequence of “b”s separated by optional periods:

      list = list-of-a | list-of-b .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
         A = 'a' .
         B = 'b' .
        -s = -['.']* .

This will happily, and unambigously, parse a list of “a” or a list of “b”, for example: “a..a.aa”:

                  
<list><A>a</A><A>a</A><A>a</A><A>a</A></list>

(In a more familiar example of this kind of grammar, s would be whitespace, for example, -[' ' | #a | #d | #9]*. A period is used as a separator in these examples only because it’s easier to see in the output.)

Suppose you want instead to parse a list of “a”, or a list of “b”, or a list of “a” followed by a list of “b”, all separated by optional periods. For example “a.a.bb”. This seems easy. A list becomes an optional list-of-a followed by an optional list-of-b possibly separated by periods:

      list = list-of-a?, s, list-of-b? .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
         A = 'a' .
         B = 'b' .
        -s = -['.']* .

Unfortunately, this is ambiguous. There are two possible parses:

$ coffeepot -g:list-ab.ixml a.a.bb --parse-count:all
Found 2 possible parses.
<records parses="2" totalParses="2">
<list xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
  <A>a</A><A>a</A><B>b</B><B>b</B>
</list>
<list xmlns:ixml='http://invisiblexml.org/NS' ixml:state='ambiguous'>
  <A>a</A><A>a</A><B>b</B><B>b</B>
</list>
</records>

There are two possible parses, but they’re both the same!

Because “-” is used to elide parts of the input in Invisible XML, it’s easy to forget that those elided parts are still in the parsed result. If we look at a full parse trees, including all of the generated nonterminals and marks, the difference becomes visible.

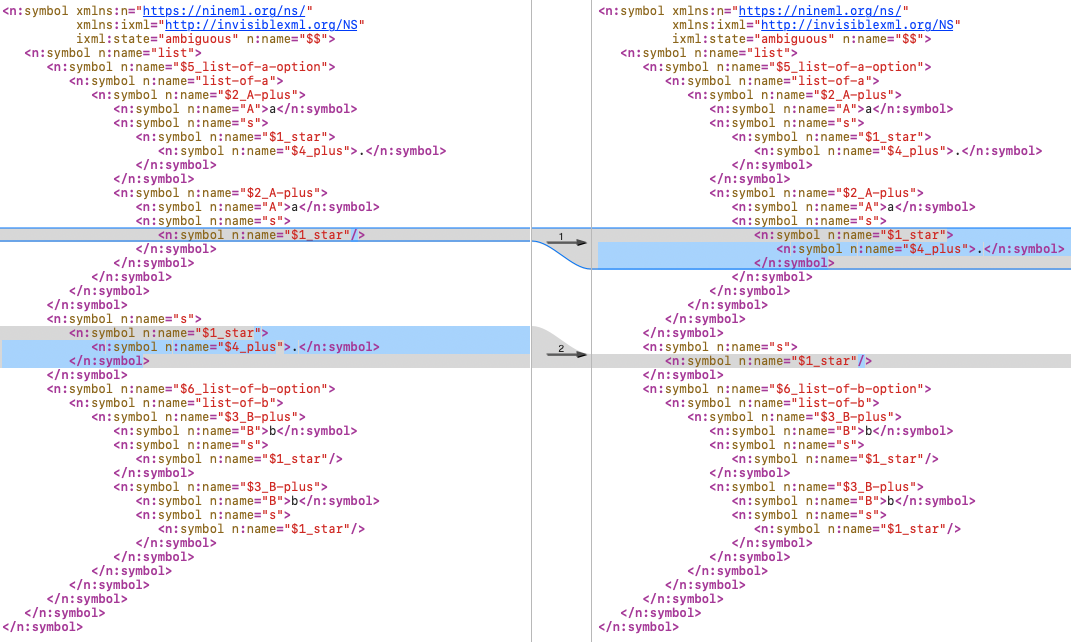
The difference is whether the “.” is consumed by the “s” in the list-of-a nonterminal or the “s” between the lists. This is horizontal ambiguity. It’s also visible in the parse forest, although the forest is getting rather large at this point. Looking at just a portion of the forest, we see:

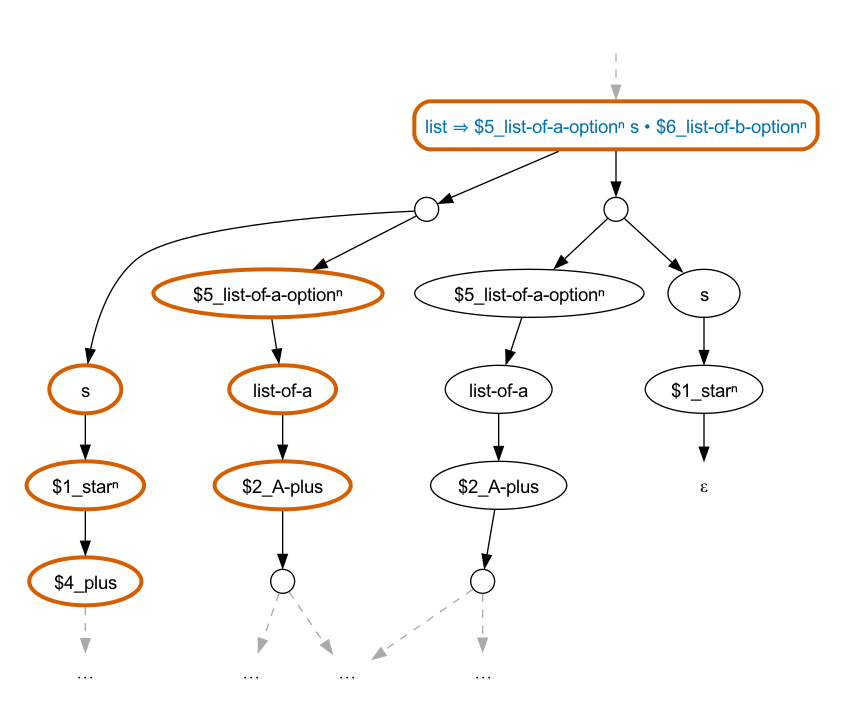
Here, the selected parse consumes the “.” in the list-of-a nonterminal, leaving the s between the lists matching the empty sequence. (The diagrams are generated with GraphViz and it’s worth observing that the order of the nodes in the diagram doesn’t always reflect the order in the input; here the selected “s” is visually on the left although in fact it occurs after the “$5_list-of-a-option”.)

If the input data is unambiguous, it is always in principle possible to write the grammar such that it is unambiguous. There are a couple of options in this grammar. Perhaps the easiest is simply to remove the s between the lists:

      list = list-of-a?, list-of-b? .
-list-of-a = (A, s)+ .
-list-of-b = (B, s)+ .
         A = 'a' .
         B = 'b' .
        -s = -['.']* .

Any periods between the last “a” and the first “b” will be consumed by the s after the A. They are elided in the output so it makes no difference how they are consumed.

Alternatively, the lists can be rewritten so that they don’t end with s, then the s between the lists is unambiguous:

      list = list-of-a?, s, list-of-b? .
-list-of-a = ((A, s)*, A)? .
-list-of-b = ((B, s)*, B)? .
         A = 'a' .
         B = 'b' .
        -s = -['.']* .

When designing grammars with optional separators, especially, for example, whitespace, it is good practices to do either one of two things:

But do not do both.

Resolving ambiguity with priorities

If your grammar can be made unambiguous, make it unambiguous. An unambiguous parse can be performed faster and will use less memory. All Invisible XML processors will produce the same results for an unambiguous parse.

If your grammar can be made unambiguous, make it unambiguous!

In an effort to address those cases where it can’t, where either the data is inherently unambiguous or the complexity of the grammar conspires to make it hard to disambiguate, the NineML suite of tools introduce an extension to Invisible XML: the ability to assign priorities to nonterminals.

Consider again the grammar for US, European, and ISO 8601 dates. Suppose you know that the overwhelming majority of your data is from the United States. You might decide that whenever a date is ambiguous, it’s a US date: that 8/1/2023 is the first of August, not the eighth of January. You want to make the usdate nonterminal “higher priority” than the eudate nonterminal.

NineML uses pragmas to assign priorities. Pragmas were introduced at Balisage 2022 in [Hillman et al. 2022b]. Pragmas are delimited with {[ and ]}, so they appear as comments to a pragma-unaware processor.

{[+pragma n "https://nineml.org/ns/pragma/"]}

                deadline = -'due', -' '+, date .
                    date = usdate | eudate | isodate .
{[n priority 2]} -usdate = month, -'/', day, -'/', year .
                 -eudate = day, -'/', month, -'/', year .
                -isodate = year, -'-', month, -'-', day .
                   month = '0'?, d | '10' | '11' | '12' .
                     day = ['0'-'2']?, d | '30' | '31' .
                    year = d, d, d, d .
                      -d = ['0'-'9'] .

The declaration at the top of the file, is a pragma that associates n with a URI. The NineML family of tools recognize that URI, so the subsequent n pragma is interpreted as a priority. (If a different URI had been used to define n, NineML would simply have ignored the pragma as unrecognized.)

In the resulting parse forest, priorities accumulate “up” the graph. At any point where a choice must be made, if one branch has a larger priority than all of the others, it will always be selected. Here is a portion of the parse forest for “1/8/2023” with this grammar:

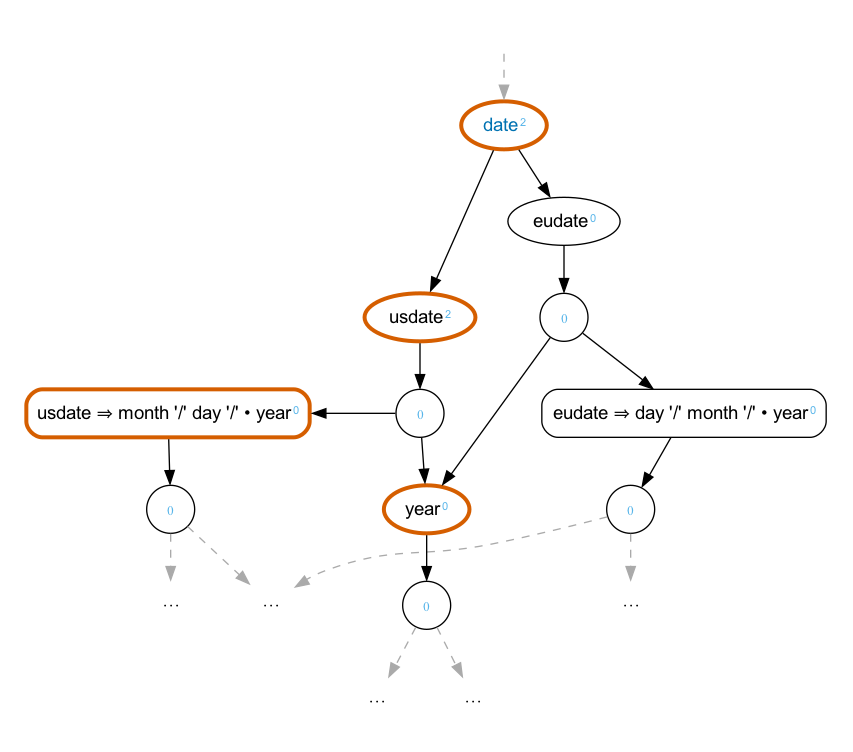
NineML will always favor the usdate over the eudate because it has the higher priority.

There are two ways to accumulate priorities. By default, the priority of any node is equal to the highest priority among the nodes below it. Alternatively, the priority can be the sum of all of the priorities below it.

This can be used to achieve some interesting effects. Consider this grammar:

{[+pragma n "https://nineml.org/ns/pragma/"]}

                 deadline = -'due', -' '+, date .
                     date = usdate | eudate | isodate .
{[n priority 4]}  -usdate = month, -'/', day, -'/', anyyear .
{[n priority 3]}  -eudate = day, -'/', month, -'/', year .
                 -isodate = year, -'-', month, -'-', day .
                    month = '0'?, d | '10' | '11' | '12' .
                      day = ['0'-'2']?, d | '30' | '31' .
                  anyyear = d, d, d, d .
                     year = newer | older .
{[n priority 2]}   -newer = '2', d, d, d .
                   -older = '1', d, d, d .
                       -d = ['0'-'9'] .

Using the default accumulation strategy, the usdate will always be preferred. However, if the summing strategy is used, eudates will be preferred for years 2000 and beyond:

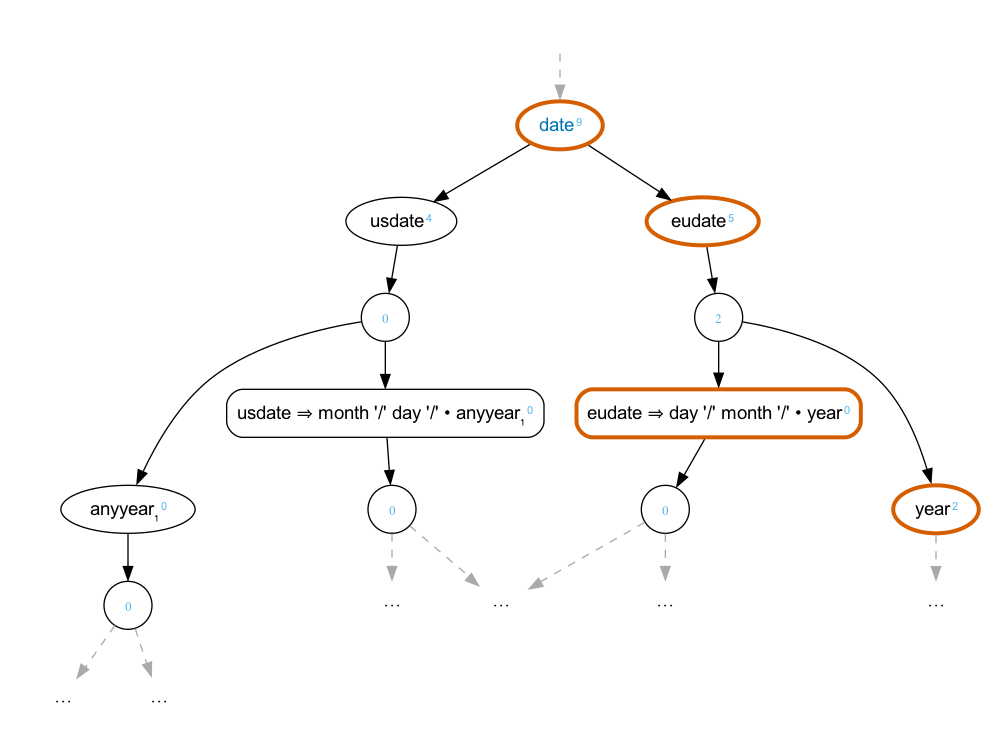
It’s critical to observe that priorities in NineML are used when selecting a tree from the parse forest. They have no effect on the parsing. It might be possible to change the actual parsing algorithms to take account of priorities, but that’s not what NineML does.

Resolving horizontal ambiguity

Applying priorities does not immediately give us a mechanism for resolving horizontal ambiguity because there’s nowhere to hang the priorities. The ambiguity in the earlier “xay” example is between two of the intermediate states. Neither a priority on A nor a priority on B will resolve it.

We can, however, introduce new nonterminals to turn the horizontal ambiguity into vertical ambiguity. Consider:

{[+pragma n "https://nineml.org/ns/pragma/"]}

                   S = "x", A, B .
                   A = A1 | A2 .
{[n priority 1]} -A1 = "a" .
                 -A2 = () .
                   B = "a", "y" | "y" .

In this grammar, the alternative that favors A matching “a” will always be selected.

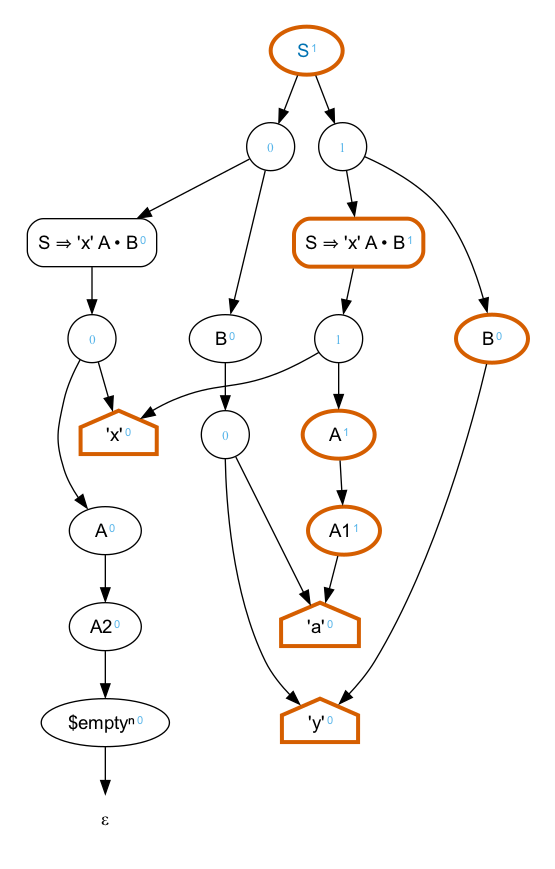
Moving the higher priority to A2 would have the opposite effect. A similar transformation applied to B would also disambiguate the alternatives.

Conclusions