This paper describes the use of invisible XML to solve a problem arising in the preparation of an electronic book version of Gottlob Frege’s 1879 pamphlet Begriffsschrift (concept writing). On many accounts, Frege’s work marks the beginning of modern logic, but the two-dimensional notation which gives the book its title poses some challenges for data capture. Most alarmingly, it is not obvious at first glance where the transcriber should begin and where they should end: Frege’s notation exploits both dimensions of the writing surface, but for keyboarding it would be helpful to reduce the two-dimensional input to a one-dimensional linear sequence. Invisible XML provides a convenient way to define an ad-hoc language for transcribing Frege’s formulas.[1]

The first section of the paper provides some background on Frege’s notation (section “Background”); the second section defines the problem to be solved (section “The problem”). The third section describes the use of invisible XML to solve the problem (section “The solution”). A final section describes some additional uses of the digitized formulas that go beyond the initial task and identifies some follow-on work to be done in the future (section “Extensions and follow-on work”).

Background

Oversimplifying slightly, the consensus of those concerned with formal logic is that formal logic in its modern form was introduced by the German mathematician Gottlob Frege in 1879 in his book Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (Frege 1879). The title can be translated as Concept writing [or: concept notation, or: concept script, or even: ideographic script]: a formula language for pure thought, modeled on that of arithmetic. Frege used his notation in his two-volume work on the fundamental laws of arithmetic (Frege 1893), which attempted to show that numbers and arithmetic can be derived from purely logical assumptions without appeal to empirical observation and which influenced the similar efforts of Russell and Whitehead in their Principia mathematica.

It must be noted, however, that logicians and historians of logic appear to cite Frege’s work somewhat more frequently than they read it. And although late in life Frege thought of his conceptual notation as his most lasting achievement, he appears to be the only student of logic who ever used it in published work. When historians of philosophy describe it, words like idiosyncratic and eccentric are deployed, and there are few efforts to explain the notation and none to use it. This is not unique to Frege: Russell and Whitehead’s notation is also increasingly distant from the way logicians now write formulas, and sometimes needs paraphrase and commentary. But Russell and Whitehead’s notation mostly looks archaic; Frege’s notation is completely foreign.

When logicians claim that Frege created modern logic in 1879, they probably have in mind things like his rejection of the traditional subject + predicate analysis of propositions (traditional since Aristotle) in favor of an analysis of propositions in terms of functions and arguments (similar in crucial ways to the functions and arguments of mathematics, and for that matter of computer programming), his introduction of an operator for universal quantification, and his approach of constructing his logical system on the basis of a very small set of primitive logical operators (material implication, negation, and universal quantification). Contrary to his own evaluation of his work, his notation, like some aspects of the notation of Peano and Russell and Whitehead, is not regarded as his major contribution.

Some time ago the author of this paper conceived the idea of republishing the book in ePub format (IDPF/W3C 2019), to make it more readily available to students. The 1879 book is rather short -- more a booklet than a book -- and its high historical interest makes it seem an ideal candidate for such a project.

It is clear on even a casual examination of Frege’s text, however, that the project is not a quick or simple one. A sample page from a scan of the copy of Frege’s book held in the Bibliothèque nationale may make the problem clear.

Figure 1

Some aspects of the page are perfectly familiar in technical writing and other academic writing: numbered sections (here §16 at the beginning of the page), displayed formulas with numbers (here, numbers on the right margin mark formulas 8 and 9), the mixture of prose text with display material, and even the use of inline formulas.

But the formulas themselves appear to defy description, and even more so to defy transcription. We see italic Roman letters (a, b, c, d) running down the right side of each formula, and they are connected by a network of horizontal and vertical lines whose meaning, if they have one, is unclear to the casual observer.

It is perhaps no wonder that the reviewers of Frege’s book found his notation off-putting. It is not just that it was unfamiliar. Any new notation is unfamiliar, but mathematics is full of work which introduces new notations. Not all of them are rejected as decidedly as Frege’s was. But at a first approximation, mathematical notation is by and large linear. It can be written left to right, and when an equation gets too long to fit on a line it can be broken over two lines in much the same way as prose. There are non-linear components and other complications in standard mathemtical notation, of course: individual symbols may be decorated with subscripts and superscripts, symbols from non-Latin alphabets can be pressed into service, new operators of unfamiliar shape may be introduced. But to a large extent, equations have a left-hand side, an equals sign, and a right-hand side, and they can be read aloud or transcribed by starting at the left and working towards the right. There are certainly mathematical notations which are not purely linear: matrix notation, summations, integrals, and so on. Note that all of these are associated with somewhat advanced mathematics and that all of them create identifiable expressions which can in turn be integrated into a linear flow. Also, notations like that for summations and integrals have a fixed number of argument positions.

Earlier nineteenth-century works on logic, like that of Boole, used an essentially similar linear notation; Boole even borrowed the conventional notation for addition and multiplication to represent logical disjunction and conjunction. Frege, by contrast, exploits the two-dimensionality of the writing surface in ways that are unfamiliar. His two-dimensional structures appear to have a variable number of argument positions, and to have more internal variation than other two-dimensional mathematical notations have. There is no real opportunity to apply habits acquired in other reading, no transfer of training. This may or may not explain the failure of others to adopt Frege’s notation, but it does seem to represent a problem for the would-be transcriber who would like to spend an hour or so in the evenings typing in a few pages of the book, until a usable electronic text is created.[2]

The problem

The problem as it presented itself to the author is fairly simple to describe: to make an XML version of Frege’s book, how on earth do we capture the diagrams? And once they are captured, how do we display them?

One possibility is to treat the formulas as graphics; this is not unheard of in ebook publication. The quality of the available images speaks against using extracts from them in that way: as the reader can observe by consulting the page reproduced above, not all of the horizontal and vertical lines are registered clearly in the scan; some are interrupted, and a few have disappeared entirely.[3] And as users of ebooks will be aware, treating formulas as graphics leads to a variety of inconveniences. When the user switches the book to night mode, or sets a sepia background, or changes the font size, formulas digitized as graphics often stubbornly refuse to change; this is particularly distracting when graphics have been used as a substitute for unusual characters by publishers who do not really trust Unicode fonts. In a commercial project, perhaps deadline pressure would force the use of the formulas-as-graphics approach. But this is not a commercial project and the author had the luxury of postponing further work on the ebook until a way could be found to represent the formulas in a more congenial way.

The requirements and desiderata for the project are these:

  1. There should be a natural XML representation of Frege’s notation, expressible as an extension to the TEI vocabulary.[4]

    The XML representation should ideally focus on the meaning of the formula and not on its layout, in order to make it possible to generate representations of the formulas in conventional logical form.

  2. It must be possible, from the XML representation, to generate acceptable SVG representations of the formulas in Begriffsschrift, suitable for use in an EPub-conformant electronic book.

  3. Experiment suggested that entering the formulas directly in such an XML representation would be tedious, time consuming, and error-prone.

    So there should be an input language, comparatively easy to keyboard,[5] which can be translated mechanically into the appropriate XML. The input language will be used only for Frege’s concept notation, so it can be simple and specialized.

  4. The translation from the language used for keyboarding into the desired pure representation may be done in a single step or in multiple steps; there may thus be multiple XML representations, some closer to the data-capture format and some closer to a general-purpose representation of logical formulas.

    It is neither a requirement nor a desideratum to have just one XML representation; equally it is not a requirement or a desideratum to have more than one.

  5. Brevity in the input language is helpful but less important than clarity and simplicity: the keyboardist should be able to focus on transcribing the formula, not on trying to remember the rules for the input language.

The solution

In order to make a usefully processable representation of Frege’s notation, the first task is to understand it better. Then the task of representing it in a keyboardable form can be undertaken.

Before proceeding to a discussion of the use of invisible XML in this project, therefore, it will necessary to spend some time outlining the meaning of Frege’s notation, for several reasons. Without some understanding of the notation, it will be hard for the reader to understand the examples or the design of the invisible-XML grammar. And as mentioned above, it’s safe to assume that with few exceptions almost no one now living is actually familiar with Frege’s formula language. And finally, the author has developed such a strong enthusiasm for Frege’s notation that he cannot resist the temptation to explain it and show other people some of its virtues. Those who do not find questions of notation and two-dimensional layout interesting are given permission to skim.

Understanding the notation

Survey of the notation

The fundamental goal of the notation is to make explicit the logical relations among ideas. In that regard it is similar to the philosophical language often imagined by Leibniz, who hoped by that by relating each complex content to the primitive ideas from which it was compounded it would be possible to achieve greater clarity and more reliability in reasoning. Unlike Leibniz, however, Frege does not appear to contemplate an alphabet of all possible primitive ideas. Instead, he assumes that those ideas will be expressed in a suitable form developed by the appropriate discipline, and that the concept notation will be used to express logical connectives. In the foreword to the 1879 book, Frege mentions the symbolic languages of arithmetic, geometry, and chemistry as examples. Part III of the book is devoted to developing some ideas relevant to the foundations of mathematics, using in part standard mathematical notation (e.g. for function application) and in part notations invented by Frege and not (as far as I can tell) part of Begriffsschrift proper. In Parts I and II, however, when introducing his notation and developing some general logical rules (what he refers to as laws of pure thought), Frege uses uppercase Greek and lowercase italic Latin letters to represent primitive (and atomic) propositions.

A full presentation would probably exceed the patience of the reader, but the essentials of Frege’s notation as presented in 1879 can be summarized fairly simply.[6] We introduce the major constructs of the notation, with examples.

Basic statements. The basic units of a formula are sentences which can be judged true or false, more or less what modern treatments of logic would call propositions.[7] As noted, Frege does not specify a language or notation for these; in practice, most of the formulas in the book use variables to represent the basic statements: uppercase Greek letters (e.g. Α, Β, Γ) in the initial presentation of the notation, later often lowercase italic Latin letters (a, b, c, ...). Some basic statements take the form of function applications, or predicates with one or more arguments; here, too, both the functors and the arguments are typically represented by variables (e.g. Φ(Α), Ψ(Α, Β), and later Ψ(a) and similar). It should be noted that applying the notions of function and argument in logical contexts was one of Frege’s most important and far-reaching innovations. Equivalence claims of the form (Α ≡ Β) also appear as basic statements. (As may be seen, basic statements are not necessarily atomic.)

Affirmation. Given a proposition (e.g. Α), it is possible to signal explicitly that one believes the proposition to be true. In Frege’s notation, this is signaled by a horizontal line to the left of the proposition, with a vertical stroke at its left end.

Figure 2

To denote the proposition without expressing any view of its truth, the vertical stroke (the affirmation stroke) is omitted.

Figure 3

The horizontal line (content stroke) can be rendered roughly as the proposition that .... (In Frege 1893, Frege dropped the name content stroke and explained the horizontal line as a function which maps a proposition, or a truth value, to a truth value. This change has implications for what we would call the type system which are interesting but which cannot be pursued here.)

Note: In some discussions, the affirmation stroke is glossed as a claim that the statement is provable, not simply that it is true, perhaps because a speaker’s attitude towards the truth or falsity of a statement is in general a psychological question with little direct relevance to the actual truth or falsity of the statement.

Conditionals. The main logical connective of the Begriffsschrift is what is sometimes called material implication, in logic textbooks written variously as ⇒ and ⊃ (or with other symbols). The sentence Β ⇒ Α is false in the case that Β is true and Α false, and otherwise it is true. Frege renders this thus:

Figure 4

As can be seen, the antecedent Β is written directly below the consequent Α, and each has a content stroke. The two content strokes are joined by a vertical line (a conditional stroke) and a sort of T junction, and the conditional has its own content stroke to the left of the T junction. The horizontal line across the top of the formula is thus divided into two parts: the part to the right of the conditional stroke represents the proposition that Α, and the part to the left represents the proposition that Β implies Α.

Composition of conditionals. Conditionals can be combined, by joining the content strokes of the antecedent and consequent with a new conditional stroke. We can thus combine Β implies Α with a third proposition Γ, to form a compound conditional. The identity of the antecedent and consequent will be evident from the position of the conditional stroke which joins them. Thus

Figure 5

is visibly a conditional whose antecedent is Γ and whose consequent is Β implies Α, or in linear notation ((Γ ⇒ (Β ⇒ Α)), while

Figure 6

has the nested conditional as the antecedent and Γ as the consequent, in linear notation ((Β ⇒ Α) ⇒ Γ).

Inference. Frege describes one and only one rule of inference, which corresponds to the traditional inference called modus ponens. From (the truth of) a conditional and the antecedent of that conditional, we can infer the consequent of the conditional. In principle, one can write out an inference step by listing the two premises, then drawing a horizontal rule and writing the conclusion below the horizontal rule. Writing out an inference in full thus entails writing both the antecedent and the consequent of the conditional premise twice; to save trouble, Frege allows theorems already proved (and given numbers) to be used as premises by reference: the number of the theorem is given to the left of the horizontal rule. In practice, Frege also makes use of a rule allowing consistent substitution of new terms for variables in a theorem, giving tables of substitutions in the left margin of an inference. A typical example may be seen at the bottom of the page given above.

Negation. In Frege’s notation, negation is indicated by a short vertical stroke descending from the content line. To the right of the stroke, the content line is that of the proposition being negated, and to the left it is the content stroke of the negation. (In Frege 1893, negation is simply a function that maps each truth value to its opposite.) The denial of a proposition Α, or equivalently the proposition that Α is false, is represented thus:

Figure 7

To assert that Α is false, we can add an affirmation stroke:

Figure 8

Universal quantification. Logic has dealt with quantifiers like all, some, not all, and none since Aristotle. Since the introduction of algebraic notation, mathematics has used formulas like x × (y + z) = x × y + x × z) with the understanding that such formulas are to be understood as holding for all values of the variables x, y, and z.

One of Frege’s important innovations in logic was to introduce notation explicitly introducing a variable like x, with the meaning for all values of x, it is the case that ..., with an explicitly understood scope for the binding of x, which was not necessarily the entire formula. The rules for working with variables of limited scope are subtly but crucially different from those governing variables whose scope is the entire formula — different enough that Frege uses distinctive typographic styling for the two kinds of variables. Variables written as letters of the Latin alphabet (invariably in italic) are implicitly bound throughout the entire formula, while variables written in Fraktur have meaning only within the scope of an explicit universal quantification.[8] The conventional formula (∀ a)(Χ(a)) can thus be written as:

Figure 9

Since the explicit universal quantifier immediately follows (i.e. is immediately to the right of) the affirmation stroke, the formula just given is equivalent to a formula using an implicit universal quantification for a:

Figure 10

Other topics. The summary just given reflects Frege’s account of the notation as given in Part I of Frege 1879, but omits some further development given in passing in Parts II and III of the book. The major omissions are:

  1. formula numbers provided for theorems

  2. the labels on premises given explicitly to show the formula number of the premise

  3. tables showing how premises used in an inference are derived by substitution from the formula whose number is given

  4. a notation allowing new notations to be defined in terms of pure Begriffsschrift expression

  5. several uses of that notation to introduce compound symbols meaning property F is inherited in the f-series, y follows x in the f-series, y appears in the f-series beginning with x (i.e. y is either identical to x or follows x in the f-series) the operation f is unambiguous (i.e. f is a function).

These all have substantive interest, and some of them pose a challenge for the task of generating suitable SVG to display them, but the only serious problem they pose for the design of the data capture notation is understanding the meaning of the new notations well enough to provide plausible linear forms for them.

Discussion

One of the frequent criticisms of Frege’s notation is the observation that any formula typically takes more space on the page as Frege writes it than it would take if written in a more conventional linear style. The simple formula Β implies Α (or equivalently Β only if Α) would be written by Russell and Whitehead as Β ⊃ Α. The formula takes two lines in Frege’s notation (with or without the affirmation stroke):

Figure 11

The sixth axiom of Principia Mathematica takes one line in the notation

(q ⊃ r) ⊃ [(p ∨ q) ⊃ (p ∨ r)]

but expands to take six lines in Begriffsschrift:

Figure 12

It is easy to see why Frege’s contemporaries and successors have judged the notation unpromising and wasteful of space.

It should be noted, however, that Frege regarded formulas like these as artificially simple. His expected application of the notation was to construct proofs related to the foundations of mathematics, in which the conditions of validity should be explicitly stated; a typical formula chosen at random from the Grundgesetze may involve eight or ten or more basic statements, each represented not by a single variable but by a mathematical formula of five or ten characters.

For such formulas, the comparison of Frege’s notation and linear notation is more complex. Consider, for example, the following formula from page 32 of Frege’s book:[9]

Figure 13

In conventional logical notation, this would be written in much less space:

((b ⇒ a) ⇒ ((c ⇒ (b ⇒ a)) ⇒ ((c ⇒ b) ⇒ (c ⇒ a)))) ⇒ (((b ⇒ a) ⇒ (c ⇒ (b ⇒ a))) ⇒ ((b ⇒ a) ⇒ ((c ⇒ b) ⇒ (c ⇒ a))))

But now consider another formula of similar size. Is this the same as the previous formula, or different?

((b ⇒ a) ⇒ ((c ⇒ (b ⇒ a)) ⇒ ((c ⇒ b) ⇒ (c ⇒ a)))) ⇒ ((b ⇒ a) ⇒ (c ⇒ ((b ⇒ a) ⇒ ((b ⇒ a) ⇒ ((c ⇒ b) ⇒ (c ⇒ a))))))

Different readers may experience different results, but I expect many readers will find it hard to tell without careful examination and the counting of parentheses whether the conventional linear formula just given is the same as that given earlier, or different.

Many readers, on the other hand, may find it easier to detect the difference (a change in parentheses) by comparing the equivalent formula in Frege’s notation to the one above:

Figure 14

A quick look at the horizontal lines across the top of the two formulas shows that they have different numbers of what might be called top-level conditionals.

As this example illustrates, Frege’s notation provides a compact visual representation of the structure of the formula, analogous to that provided by a parse tree for any string described by a suitable grammar, and also at least roughly analogous to the structure made explicit in the element structure of an XML document.

In fact, Frege’s notation is not just like a parse tree. It can be most easily read as a parse tree, for a particular logical syntax, with the root drawn at the upper left instead of the top center, and the leaves written vertically in sequence down the right-hand side of the diagram instead of horizontally across the bottom. Compared to linear notations, parse trees do take more space. Compared to other parse-tree notations, Begriffsschrift is noticeably more compact than most.

Consider the conventional linear representation for Frege’s theorem 2:

(c ⇒ (b ⇒ a)) ⇒ ((c ⇒ b) ⇒ (c ⇒ a))

A parse tree for this expression, drawn more or less conventionally, might look like this:

Figure 15

If rotated 45 degrees counter-clockwise, it might look like this:

Figure 16

Arranging all the leaves vertically on the right we have:

Figure 17

And if we now replace diagonal lines with vertical and horizontal lines, we have something that bears a striking visual resemblance to Frege’s notation:

Figure 18

The actual form of this expression in Begriffsschrift is:

Figure 19

The shape of the tree is identical; the only change is that the internal nodes denoting conditionals are not labeled. They need no labels: since there is only one binary operator in the language, any internal node in the tree with two nodes is a conditional. Negation and universal quantification are unary operators and have only one child; so also affirmation (which in any case occurs only as a sort of annotation on the root of the tree).

Writing the leaves top to bottom instead of left to right also has the effect of reversing the order of the children of conditional nodes, which works out conveniently here since Frege writes the consequent before (above) the antecedent. His practice gives visual prominence to the consequent of the sequence of conditionals, which is likely to be of more interest for the argument being developed than the antecedent(s).

Like any parse tree, Frege’s notation makes the structure of an expression much easier to perceive than a linear notation with multiple levels of nested parentheses.

The relation between Frege’s notation and parse trees appears to have passed unnoticed (or at least unmentioned) until recently, but has now been independently observed and usefully discussed by Dirk Schlimm (Schlimm 2018). For what it is worth, the author’s experience suggests that it is much easier to learn to understand Begriffsschrift formulas fluently by reading them as parse trees than by attempting to translate them mentally into conventional notation.

Using ixml to define the data capture language

One obvious natural representation of Frege’s notation would be an XML vocabulary for the representation of conventional first-order logic, with elements for propositional variables and other basic statements, and for the various logical operations: negation, conjunction, disjunction, material implication, and quantification. In transcribing Frege, only basic sentences, material implication, negation, and universal quantification would be used. The representation is natural enough, but the idea did not survive contact with even simple examples: even for a user with long experience editing XML documents, data entry was very cumbersome.

A second possibility was to record each formula not in XML but in an easily keyboardable representation of conventional logic. Formula 2 (used as an example in the discussion of parse trees above) might be represented as (c implies (b implies a)) implies ((c implies b) implies (c implies a)). A post-processing step would be needed to parse this into the XML form, but the syntax is not very complicated and writing a parser would be an interesting exercise. This approach worked a little better than direct entry of the XML, but it was found cumbersome and error prone. Transcribing the antecedent of a conditional before the consequent requires reading Frege’s formulas bottom to top, as it were, and the correct placement of parentheses was a constant challenge.

The key step towards a simpler notation came with the realization that Β implies Α can also be verbalized as if Β, then Α, and the order can be reversed to put the consequent first if we just say Α if Β. And indeed Alpha if Beta is the form taken by the formula

Figure 20

in the data capture language developed for this project. (It will be convenient to give the language a name; in the remainder of this paper it will be referred to as kB for keyboardable Begriffsschrift.)

Perhaps the easiest way to introduce kB is to give the kB equivalents for the examples given in the survey above, and to introduce the key ixml definitions for each construct. (The full ixml grammar is given in an appendix.)

Variables. Uppercase Greek letters may be entered directly or spelled out: Α, Β, Γ can be entered as Alpha, Beta, Gamma. Variables spelled with italic Latin letters have an asterisk before the letter itself (so F and f are spelled *F and *f); for lower-case letters, the asterisk is optional.[10] Fraktur letters may be written directly (using the mathematical Fraktur characters of Unicode / ISO 10646) or with a preceding f or F: 𝔣 and 𝔉 are written ff and FF.

In each case, the translation of the string into the appropriate character sequence is handled by marking the data capture form using - (hide) and inserting the form that should occur in the XML produced by the ixml parser. So the rule for upper-case Greek letters takes the form: 

-Greek-letter: [#391 - #03A9] { 'Α'-'Ω' }
             ; -'Alpha', + #0391 {'Α'}
             ; -'Beta', + #0392 {'Β'}
             ...
The first line of the production rule accepts any upper-case Greek character typed by the user; the later lines accept the names of the characters, written with an initial capital, suppress the string typed by the user and insert the appropriate Greek character.

The rules for Fraktur and italic are handled similarly: 

-italic: (-'*')?, ['a'-'z'].
-Italic: -'*', ['A'-'Z'].

-fraktur: [#1D51E - #1D537]
        ; -'fa', + '𝔞' {#1D51E}
        ; -'fb', + #1D51F
        ; ...
        .
-Fraktur: [#1d504 - #1d51d] { not all letters are present! }
        ; -'FA', + #1D504 {'𝔄'}
        ; -'FB', + #1D505 {'𝔅'}
        ; ...
        .
These simple short-forms are possible without conflict because no variable name in Frege’s book is more than one character long. So using fa to denote Fraktur a or 𝔞 does not conflict with any other possible uses. This is an advantage of devising an input format for such a specialized usage.

These various forms are gathered together as varying possible expansions of the nonterminals var and bound-var. 

var:  Greek-letter; italic; Italic.
@bound-var: fraktur; Fraktur.
The distinction between the two non-terminals is not strictly necessary but it may make it easier to check that no Fraktur variables are used outside the scope of their quantifier.

Function applications. Function applications are written in the obvious way. In Frege’s book, no concrete functions actually appear in any formulas (other than the identity function ≡, which is written with infix notation): all function applications use variables both for their arguments and for the function name. By convention, Frege writes function names with upper-case variables (Greek, italic Latin, or Fraktur); arguments use upper-case Greek, lower-case italic Latin, and lower-case Fraktur. So Φ(Α), Ψ(Α, Β), and later Ψ(a) are encoded in kB as Phi(Alpha), Psi(Alpha, Beta), and Psi(a).

Affirmation. In kB, the presence of an affirmation stroke is signaled by the keyword yes at the beginning of the formula. The absence of the affirmation stroke may optionally be explicitly signaled using the keyword maybe.

So yes Alpha is the kB encoding of

Figure 21

And the formula

Figure 22

can be encoded either as maybe Alpha or just as Alpha.

Conditionals. In kB, the keyword if takes the consequent as its left-hand argument and its antecedent as its right-hand argument; it is thus the converse of conventional implication (⇒ or ⊃). The formula

Figure 23

is transcribed

Alpha if Beta

So in kB the left-right order of basic statements matches their top-to-bottom order in Frege’s notation.

Composition of conditionals. The kB if keyword is left-associative, so the formula

Figure 24

is transcribed in kB as:

Alpha if Beta if Gamma

Parentheses are used for the case where the antecedent itself is a nested conditional: the formula

Figure 25

is transcribed

Gamma if (Alpha if Beta)

As an empirical matter, in Frege’s formulas nested conditionals more frequently occur in the consequent than in the antecedent of other conditionals, so making if left-associative saves a considerable number of parentheses. A similar saving could be achieved in conventional notation for these formulas, if the material implication were taken to be right-associative. In practice, definitions of conventional logical syntax typically require parentheses for all nested conditionals.

The rules used in ixml to make conditionals left-associative interact with other operators and will be discussed below.

Inference. The simple form of an inference simply lists both premises and the conclusion. Frege gives this example:

Figure 26

The kB transcription of this is: 
we have: yes Alpha if Beta
    and: yes Beta
from which we infer: yes Alpha.
For the case where either premise becomes long and complicated, an optional comma is allowed after it to help the human reader understand the structure of the formula more easily.

In practice, Frege’s inferences typically replace one of the premises with a numeric reference to that premise which appears parenthetically to the left of what may be called the inference line (the horizontal rule separating premises from conclusion), followed by either one or two colons. One colon means the elided premise is the first premise in the modus ponens, a conditional; two colons means the elided premise is the second one, which matches the antecedent of the first premise. Here is Frege’s example of the second form, assuming that formula XX asserts the truth of Α:

Figure 27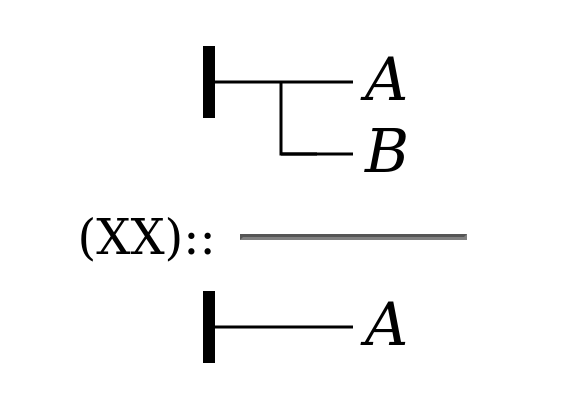

The kB representation uses the keyword via to introduce the elided premise: 
we have: yes Alpha if Beta,
from which via (XX)::
we infer: yes Alpha.

Further elaborations allow multiple inference steps each of which elides one premise. Overall, the rules for inferences are thus the most complex seen so far: 

inference:  premises, sep,
            infstep++sep.

-premises:  -'we have:', s, premise++(sep, -'and:', s).

infstep: -'from which', s,
         (-'via', s, refs, s)?, 
         -'we infer:', s, conclusion.

premise:  formula.

conclusion: -formula.

-refs: premise-ref-con; premise-ref-ant.
premise-ref-con:  -'(', s, ref++comma, s, -'):'.
premise-ref-ant:  -'(', s, ref++comma, s, -')::'.

ref: 'X'+; ['0'-'9']+.
The nonterminal sep identifies a separator: either whitespace or a comma followed by whitespace: 
-sep: ss; (-',', s).

The XML being produced by all of these grammar rules follows naturally from the rules of invisible XML, but perhaps an example should finally be given. This is the XML produced by the sample inference shown just above. 

<inference>
   <premise>
      <formula>
         <yes>
            <conditional>
               <consequent>
                  <leaf>
                     <var>Α</var>
                  </leaf>
               </consequent>
               <antecedent>
                  <leaf>
                     <var>Β</var>
                  </leaf>
               </antecedent>
            </conditional>
         </yes>
      </formula>
   </premise>
   <infstep>
      <premise-ref-ant>
         <ref>XX</ref>
      </premise-ref-ant>
      <conclusion>
         <yes>
            <leaf>
               <var>Α</var>
            </leaf>
         </yes>
      </conclusion>
   </infstep>
</inference>

Negation. In keeping with the general trend of trying to let the transcriber keep their fingers on the keyboard characters, kB uses the keyword not to encode negation, in preference to other symbols often used for negation (~, ¬, !, ...). The negation

Figure 28

is encoded

not Alpha

and the formula

Figure 29

is encoded

yes not Alpha

Since negation is a unary operator, it must be right-associative (unless we want double negation to require parentheses, which we do not). But its binding strength relative to other operators interacts with the rules for those other operators and so the ixml rules for negation will be discussed and given below.

Universal quantification.

The conventional formula (∀ a)(Χ(a)) can be written as:

Figure 30

In kB, it is written using the keywords all and satisfy:

yes all fa satisfy Chi(fa)

Associativity and binding. In order to define rules for conditionals, negation, and universal quantification which work acceptably, it is necessary to consider how they interact. In technical terms, we must consider the binding strength and associativity of the relevant operators. In less technical terms, we must decide what structure should be inferred when ... if ..., not ..., and all ... satisfy ... occur together without parentheses to show the desired structure. For some examples, the desired structure seems obvious; there may not be any plausible alternative:

not not Alpha

not all fa satisfy Phi(fa)

all fa satisfy not Phi(fa)

not all fa satisfy not Phi(fa)

all fa satisfy all fd satisfy Phi(fa, fd)

all fa satisfy not all fd satisfy not Phi(fa, fd)

not all fd satisfy not all fa satisfy Phi(fa, fd)

Alpha if not Beta

Alpha if not all fa satisfy Phi(fa)

Beta if all fa satisfy not Phi(fa)

Gamma if not all fa satisfy not Phi(fa)

If these examples are legal, it is obvious what structure they must have; the only alternative would be to require that explicit parentheses be used:

not (all fa satisfy (Phi(fa)))

all fa satisfy (not (Phi(fa)))

not (all fa satisfy (not (Phi(fa))))

etc.

These parenthesized forms should of course be allowed, but ideally not required.

For some combination forms, we have already decided how they should be parsed. Nested conditionals should be handled as described above, so

Alpha if Beta if Gamma

should be equivalent to

(Alpha if Beta) if Gamma

and not to

Alpha if (Beta if Gamma)

A more serious design question arises with the possible interactions of conditionals with the other two operators. How should examples like these be parsed?

yes not Alpha if Beta

all fa satisfy Phi(fa) if Gamma

In most programming languages, and in most forms of symbolic logic, negation is held to bind more tightly than the conditional, so yes not Alpha if Beta should probably be interpreted as yes (not Alpha) if Beta

Figure 31

and not as yes not (Alpha if Beta)

Figure 32

So for negation and conditional, a simple rule seems possible: conditionals can govern unparenthesized negations in both antecedent and consequent, but negation never governs an unparenthesized conditional.

For conditionals and universal quantification, both possible rules seemed plausible. On the one hand, the syntax may be easier to remember if the rule for quantifiers and the rule for negation are the same. So perhaps all fa satisfy Alpha if Beta should be parsed as (all fa satisfy Alpha) if Beta). On the other hand, quantifiers tend to be introduced late in the exposition of any syntax, and operators introduced late typically bind loosely. So perhaps all fa satisfy Alpha if Beta should be parsed as all fa satisfy (Alpha if Beta).

If one form of construct were dramaticaly more common than the other, it would be natural to encode the more common construction without parentheses. But a brief examination of examples suggested that in Frege’s formulas, the number of quantifiers which govern conditionals and the number of quantifiers which appear in the consequent of conditionals were roughly comparable. So neither choice will save a dramatic number or parentheses.

A third possibility was also considered: if it is this hard to choose the relative binding strength of all ... satisfy ... and ... if ..., then perhaps parentheses should be required either way, and the construct all fa satisfy Alpha if Beta should simply be a syntax error.

In the end, the arguments of simplicity won. In this case, simplicity took two forms. First, making universal quantification behave the same way as negation seemed to be simpler to remember; the rule is simply that neither unary operator governs an unparenthesized conditional. And second, making the two unary operators behave the same way made the formulation of the grammar easier.

The basic requirement is that in some contexts, any proposition should be allowed, while in other contexts, unparenthesized conditionals are not allowed but any other propostion is syntactically acceptable. We thus define rules for three kinds of propositions. 

-prop-no-ifs:  leaf; not; univ; parenthesized-prop.
-proposition: prop-no-ifs; conditional.
-parenthesized-prop: -'(', s, proposition, s, -')'.
The nonterminals not and univ are defined below. The nonterminal leaf covers all basic statements (the name leaf is shorter than basic_stmt). Here, too, the nonterminal could be hidden, but it turns out to be convenient to have a single element type as the root of every basic statement.

With the help of the two nonterminals proposition and prop-no-ifs, we can now define the various mutually recursive compound operators. Conditionals have a consequent and an antecedent. These could be marked hidden to make the XML syntax simpler, but it’s convenient for some purposes to be able to select consequents using an XPath expression like ./consequent rather than ./*[1]. 

conditional: consequent, s, -'if', s, antecedent.
consequent: proposition.
antecedent: prop-no-ifs.
Using proposition as the definition of consequent and prop-no-ifs as the definition of antecedent has the effect of making conditionals left-associative.

Since negation never binds a non-parenthesized conditional, its definition uses prop-no-ifs. 

not: -'not', s, prop-no-ifs.

The ixml rule for universal quantifiers also uses prop-no-ifs, for the same reason. 

univ:  -'all', s, bound-var, s, -'satisfy', s, prop-no-ifs.

@bound-var: fraktur; Fraktur.

A note on whitespace handling. The handling of whitespace is one of the trickiest and least expected problems confronted by the writer of invisible-XML grammars. Even those with long experience using and writing context-free grammars may be tripped up by it, partly because most practical tools for parser generation assume an upstream lexical analyser or tokenizer which can handle whitespace rules, and most published context-free grammars accordingly omit all mention of whitespace. Because ixml does not assume any upstream lexical analyser, whitespace must be handled by the grammar writer.

If care is not taken, then either whitespace will not be allowed in places where it should be allowed, or it will be allowed by multiple rules, introducing ambiguity into the grammar. (In this case, the ambiguity is usually harmless, since the position of whitespace seldom affects the intended meaning of the input. But there is no way for the parser to know when ambiguity is harmless, so it will warn the user.) On the other hand, if care is taken, then whitespace handling can begin to consume all too much of the grammar writer’s thoughts. It would be convenient to have a relatively simple systematic approach to the handling of whitespace. So far, there appear to be two such, although neither has (as far as the author is aware) been described in writing. They may be called the token-boundary approach and the whitespace floats upward approach.

Both typically assume some nonterminal for whitespace, which for concreteness I’ll call s. I assume s matches zero or more whitespace characters, so whitespace is usually optional; if whitespace is required, the paired nonterminal ss can be used.

The two approaches can be simply described.

  1. The token-boundary approach to whitespace allows s at the end of every token in the grammar.

    This may sound unhelpful, since ixml does not assume a separate tokenizer and does not identify tokens as such. Tokens may nevertheless appear in ixml grammars, identiable as units within which whitespace is not allowed, and between which whitespace (usually) is allowed.

    In the grammar for kB, for example, the nonterminals Greek-letter, italic, etc. can be regarded as defining tokens. So in a grammar using this approach to whitespace handling, italic might have been defined as 

    -italic: (-'*')?, ['a'-'z'], s.

    Note that whitespace is not allowed at the beginning of a token; any whitespace occurring before an occurrence of italic will belong to whatever token precedes the italic variable in the input. This rule avoids ambiguity caused by whitespace between two tokens being claimed by both.

    Quoted and encoded literals are also usually tokens in the sense intended here. So in a grammar using this approach, conditional might be defined: 

    conditional: consequent, -'if', s, antecedent.
    The s must be supplied, in order to allow whitespace after the keyword.

    The specification grammar of ixml (that is, the grammar for ixml grammars, as given in the specification) is a good example of the token-boundary approach. The approach has the advantage that any rule not itself defining a token does not need to worry about whitespace, with the possible exception of the top-level rule, which must mention s as its first child, in order to allow leading whitespace in the strings recognized by the grammar.

  2. The whitespace-floats-upward approach to whitespace can perhaps best be understood as an application to ixml of a principle followed by many users of XML and SGML, which is that whitespace occurring at the boundaries of phrase-level elements belongs outside the phrase-level element, not inside it. Following this principle, many users would encode the beginning of this paragraph as 

    <p>The <term>whitespace-floats-upward</term> approach ...
    and not as 
    <p>The<term> whitespace-floats-upward </term>approach ...

    On this principle, the whitespace before and after a term (or a token) is not strictly speaking part of the token and should be outside it, not inside it.

    So in the whitespace-floats-upward approach, the basic rule is that as a rule no nonterminal begins or ends with whitespace, and if whitespace is needed at the boundaries of any nonterminal, the parent should provide it. This approach thus has the disadvantage that s is mentioned in many high-level nonterminals, which can distract readers who have not yet learned to read past it. Another drawback is that rules with optional children become more complex: instead of writing xyz? for an optional child, one must write (xyz, s)? in the simple case, and complex cases can become tedious.

    The grammar given here uses this approach.

Relation to other work

For a notation routinely declared dead, the Begriffsschrift has inspired a surprising number of tools and electronic representations.

The programming language Gottlob. There is an imperative programming language named Gottlob whose notation is inspired by Frege (Dockrey 2019, see also Temkin 2019) and which has an in-browser code editor which assists the user in constructing formulas. Parts of the code really do look like bits of formulas from Frege’s book. Unfortunately, the notation of the programming language deviates from Frege in ways that make using the editor a slightly painful experience for anyone who has internalized those rules.[11] The editor offers an export mechanism but the output is a mass of Javascript which is not really suitable for further processing (at least, not by this author). The imperative nature of the language is also a barrier: a purely declarative language in the style of a theorem prover or Prolog would suit the notation better.

TeX libraries for typesetting Begriffsschrift. There appear to be at least four TeX macro libraries for typesetting the notation; all are available from CTAN, the standard archive for TeX libraries. The first three appear to be genetically related.

  1. Josh Parsons appears to have developed begriff.sty in 2003 or so, with later changes and additions by Richard Heck and Parsons (Parsons 2005). It satisfies the basic requirement (i.e. it can be used to typeset formulas written in Frege’s notation), but it has the reputation of being a little awkward. For example, it requires the user to align the formulas on the right manually.

  2. Quirin Pamp’s frege.sty started from Parsons’s package but eventually reworked it to the point of incompatibility. It aligns the style more closely with that used by Frege’s typesetters.

  3. Marcus Rossberg developed grundgesetze.sty beginning in 2008 for use in an English translation of Frege’s Grundgesetze (Rossberg 2021). It is based on Parsons’s library, but seeks to match the typographic style of Frege 1893 rather than Frege 1879.

These all differ from the current work in two important ways. First, because they use TeX to render the formulas, they can be used to generate PDF or printed pages, but they can be used to help produce an ebook conforming to the EPub standard only if the formulas are to be presented as graphics, not if live text is desired. Second, although the authors have made a certain effort to give mnemonic names to the macros, their fundamental concerns appear to be typographic. Also, the context in which they are working imposes certain limitations on them, and the TeX formulations for formulas are not notable for their perspicuity.

As an example, consider the following formula, used as an example in Rossberg’s documentation (If F(a) holds, then there exists some 𝔞 such that F(𝔞)):

Figure 33

Using the macros of grundgesetze.sty and the native facilities built into LaTeX, this can be rendered thus: 
\GGjudge\GGconditional{Fa}
    {\GGnot \GGquant{\mathfrak a} \GGnot F \mathfrak a}
This formulation has the drawback, however, that it does not align the basic statements of the formula vertically on the right. That can be done by specifying an overall formula width and marking the basic statements as such using the \GGterm{} macro: 
\setlength{\GGlinewidth}{25.2pt}
\GGjudge\GGconditional{\GGterm{Fa}}
                      {\GGnot \GGquant{\mathfrak a} \GGnot
                       \GGterm{F \mathfrak a}}
In kB, this formula becomes yes not all fa satisfy not *F(fa) if *F(a). I will leave to others to judge if it is more easily understood: familiarity will make almost anything easily readable. But it is certainly shorter and almost certainly easier to type. In a large general-purpose ecosystem like TeX or LaTeX, short, convenient codes must be reserved for phenomena common across many texts, and the content / markup distinction must be maintained. The result is a notation that fits fine within TeX, but is a little daunting to the prospective typist.[12]

Reacting in part to the perceived shortcomings of the earlier macro libraries, Udo Wermuth developed yet another set of macros, gfnotation (Wermuth 2015). He provides both a low-level language to allow fine-grained control over the typesetting of a formula and a terser higher-level short-form language. As an example consider the formula:

Figure 34

In the short-form language, this formula is produced by the TeX code ..\gA.{*.a.{f(\da)}}. It must be admitted that this is shorter than the formulation Alpha if all fa satisfy f(fa) suggested by the work described above. It may be suspected, however, that a reader will reach fluency in reading kB than in reading Wermuth’s short-form.

Etext versions of Frege. Some traces in sources like Wikipedia suggest that there have been some efforts to transcribe Frege 1893 in electronic form, and the author has vague memories of having seen at least a partial transcript online, but the links all appear to be broken and the author’s belief that there was such an electronic text cannot be substantiated.

Pamp (Pamp 2012) writes of a plan to transcribe Frege 1879 and include it with his macro library as an illustration of the usage of the library, but the current version of the library contains no file matching that description.

Lessons learned

Some points illustrated by the work described here may be worth calling attention to.

  1. It is much easier to work with information if you understand it. It is much easier to design a shorthand representation for information if you understand it.

    Even a superficial understanding may help. At first glance, the two-dimensional notation devised by Frege seemed impenetrable to this author, but a little study, given particular focus by the task of data entry, made it possible to develop a terse and (I think) easily comprehensible linear representation of the notation.

  2. Context-free grammars allow much more convenient data entry formats than regular expressions.

    By bringing the full power of grammars to bear, we can devise a data format to handle more complex expressions than would be possible with regular expressions. By exploiting ixml’s notation for grammars, we can annotate the grammar and explain it to the maintenance programmer (that is, ourselves in a few months’ time) better than is typically feasible with regular expressions.

  3. Compact notations defined by context-free grammars may be both more compact and easier to keyboard than corresponding XML. This is particularly helpful for what Josh Lubell calls SANDs (specialized arcane non-trivial data) with high information density (and, in a useful XML representation, a high tag-to-content-character ratio). It is likely to be expecially helpful when the data format in question is recursive.

  4. Like various tag minimization features of SGML, invisible XML makes it feasible to use much deeper nesting of elements and a much higher markup-to-content ratio than is usual in tag sets designed for manual application.

    The extra tags can make later processing simpler, and can make the XML representation of the information denser and harder to read without custom display options for selective hiding of markup.[15]

  5. Small things can make a big difference in the development and use of an ixml grammar.

    Invisible-XML deletions and insertions make it possible to perform simple transliteration while parsing, as illustrated here by the treatment of Greek and of Fraktur. And a simple systematic approach to the definition of whitespace (here, the whitespace-floats-upward approach) can minimize the whitespace-related troubles of grammar development.[16]

  6. Like a schema, an ixml grammar does not need to enforce every rule.

    If downstream software will break when a rule is not followed, that rule is probably worth enforcing. But often the grammar can be slightly simpler if it allows some constructions that don’t actually occur in practice, by not enforcing some exceptions as special cases.

    In Frege’s notation, for example, both explicitly bound variables (typeset in Fraktur) and implicitly bound variables (italics) can be used as function arguments, but Fraktur variables are never used to stand for basic statements (as propositional variables), only italic variables. Frege also uses upper-case Greek variables as function arguments, but only within tables of substitutions, where they have a special meaning. The grammar is much simpler if it does not try to enforce these conventions. A more complex grammar would make it easier to catch some transcription errors, but those errors are not actually very common. Making the grammar simpler makes it easier to avoid errors in the grammar. In this case, the tradeoff is clear. Several other examples of regularities found in Frege but not enforced by the grammar are noted in the kB grammar.

  7. Even if the grammar does not enforce every rule, it may be necessary to write escape hatches into it.

    Because he is presenting a new notation, Frege from time to time discusses the notation and alternatives he has considered and rejected. At the beginning of the book, for example, he shows examples of content strokes and affirmation strokes which are accompanied by no basic statements and thus have nothing whose content and affirmation they can denote. After showing how the conditional and negation together can be used to express the logical operators AND and OR, he shows how an alternative notation based only on conjunction and negation could similarly be used to express the conditional. And towards the end of the book, he illustrates why certain subexpressions in a particular notation must be subscripted, by showing a similar expression in which they are not subscripted and discussing the problems that would arise in that case.

    Such examples of syntactically invalid forms have been ignored in the discussion here, but if an ebook is to be produced they must be handled one way or another. Either kB must be extended to include ways to express these negative cases, or they must be routed through a different secondary workflow. (Re-organizing kB to focus on typographic form and not on meaning is also theoretically an option, but it would involve giving up on most of the requirements and desiderata identified above.)

Appendix: ixml grammar in full

For reference, the full ixml grammar for the data capture language kB is given below. 

{ Gottlob Frege, Begriffsschrift, eine der arithmetisschen
nachgebildete Formelsprache des reinen Denkens (Halle a.S.:
Verlag von Louis Nebert, 1879. }

{ Revisions:
  2023-04-18 : CMSMcQ : allow page breaks in inferences.
  2023-04-05 : CMSMcQ : move on to Part III.
  2023-04-05 : CMSMcQ : move on to Part II.
                        . allow braces for parenthesized propositions
                        . support formula numbers
                        . unhide conclusion/formula
                        . allow tables of substitutions
  2023-04-01 : CMSMcQ : add italic caps (*F)
  2023-03-31 : CMSMcQ : tweaks (make functor an element)
  2023-03-29 : CMSMcQ : tweaks (hiding, Greek, Fraktur)
  2023-03-28 : CMSMcQ : everything in Part I is now here
  2023-03-27 : CMSMcQ : started again from scratch
  2020-06-23 : CMSMcQ : made standalone file
  2020-06-03/---06:  CMSMcQ : sketched a grammar in work log
}

{ Preliminary notes:

  The grammar works mostly in the order of Frege's presentation, and
  top down.

  We follow the basic principle that no nonterminal except the
  outermost one starts or ends with whitespace.
}


{ ****************************************************************
  Top level
  ****************************************************************}
  
{ What we are transcribing -- an inline expression that needs special
  attention, or a typographic display -- can be any of several things:

  - a formula expressing a proposition, either with an affirmative
    judgement (nonterminal 'yes') or without (nonterminal 'maybe'),

  - the declaration of a new notation, or 

  - an inference (one or more premises, and one or more inference 
    steps, or

  - a basic formula without a content stroke (perhaps not strictly
    to be regarded as a full formula in Frege's notation, but in
    need of transcription).

  If there are other kinds of expressions, I've missed them so far.

  After any of these, we allow an optional end-mark.  

}

-begriffsschrift: s, 
                  (formula
                  ; inference
                  ; notation-declaration
                  ; mention
                  ),
                  s, (end-mark, s)?.


{ ****************************************************************
  Formulas
  ****************************************************************}

{ A formula is one sequence of basic statements with a logical
  superstructure given by content strokes, conditional strokes,
  negation strokes, and possibly an affirmation stroke.

  As mentioned in §6 but not shown in detail until §14, formulas can
  be numbered (with a label on the right), and when used as a premise
  they can be (and in practice always are) numbered with a label on
  the left, to show where the formula was first given. Call these
  right-labels and left-labels.

  Only one label ever appears, but we don't bother trying to enforce
  that.  If two labels appear, there will be two @n attributes and the
  parse will blow up on its own.

  For that matter, only judgements carry numbers, so unless the
  formula's child is 'yes', it won't in practice get a right-label.
  But that, too, we will not trouble to enforce.

}

formula: (left-label, s)?, (yes; maybe), (s, right-label)?.

{ A right-label of the form (=nn) assigns a number nn to this formula;
  it occurs when the formula is a theorem. }

-right-label: -'(', s, -'=', s, @n, s, -')'.

{ A left-label of the form (nn=) identifies a fully written out
  premise of an inference as a theorem given earlier.  Left-labels do
  not appear in Frege's presentation of inference steps in Part I, but
  they appear on all fully written out premises in Parts II and III.

  Note that left-hand labels may have tables of substitutions, which
  are defined below with inferences.

}

-left-label: -'(', s, @n, s, (substitutions, s)?, -'=', s, -')'.

{ In left- and right-labels, the number becomes an @n attribute on the
  formula. }

@n: ['0'-'9']+.

{ ................................................................
  Propositions
}

{ §2 The content stroke (Inhaltsstrich). }

maybe:  (-'maybe', s)?, proposition.


{ §2 The judgement stroke (Urtheilsstrich). }

yes:  -"yes", s, proposition.

{ Frege speaks of content which may or may not be affirmed; in effect,
  we would speak of sentences to which a truth value may be attached.
  I think the usual word for this is 'proposition'.

  A proposition can be a basic proposition (leaf), or a conditional
  expression, or a negation, or a universal quantification.  For
  technical reasons (operator priorities, associativity) we
  distinguish the set of all propositions from the set of 'all
  propositions except unparenthesized conditionals'.

}

-prop-no-ifs:  leaf; not; univ; analytic; parenthesized-prop.
-proposition: prop-no-ifs; conditional.
-parenthesized-prop: -'(', s, proposition, s, -')'
                   ; -'{', s, proposition, s, -'}'.

{ The simplest binding story I can tell is roughly this:

  The 'if' operator is left-associative.  So "a if b if c" = ((a if b)
  if c).

  This allows a very simple transcription of formulas with all
  branches on the top or main content stroke, and allows the simple
  rule that parentheses are needed only when the graphic structure is
  more complicated (for conditionals not on the main content stroke
  and not on the main content stroke for the sub-expression), or
  equivalently: parens are needed for conditionals in the antecedent,
  but not for conditionals in the consequent.

  A very few glances at the book show that when conditionals nest,
  they nest in the consequent far more often than in the antecedent,
  so this rule coincidentally reduces the need for parentheses.

  For negation and universal quantification, right-association is
  natural.  But should "not Alpha if Beta" mean ((not Alpha) if Beta)
  or (not (Alpha if Beta))?  By analogy with other languages, negation
  is made to bind very tightly: we choose the first interpretation.
  So we say that the argument of 'not' cannot contain an
  unparenthesized 'if'.

  For universal quantification, the opposite rule is tempting: unless
  otherwise indicated by parentheses, assume that the expression is in
  prenex normal form.  That would make "all ka satisfy P(ka) if b"
  parse as (all ka satisfy (P(ka) if b)), instead of ((all ka satisfy
  P(ka)) if b).

  But I think the rule will be simpler to remember if both unary
  operators obey the same rule: no unparenthesized conditionals in the
  argument.

  So "all ka satisy P(ka) if b" should parse as a conditional with a
  universal quantification in the consequent, not as a universal
  quantification over a conditional.  Preliminary counts suggest that
  the quantification may be slightly more common than the conditional,
  but both forms are common, as are cases where a quantifier governs a
  conditional which contains a quantifier.

  So we want a non-terminal that means "any proposition except
  a conditional'.  That is prop-no-ifs.

}


{ ................................................................
  Basic propositions (leaves)
}

{ The expressions on the right side of a Begriffsschrift formula
  are basic propositions.  We call them leaves, because they are
  leaves on the parse tree.

  They are not necessarily atomic by most lights, but they are
  normally free of negation, conjunction, and other purely logical
  operators.

  For the moment, we distinguish four kinds of basic propositions:
  expressions (variables and function applications), equivalence
  statements, introduction of new notation (a special kind of
  equivalence statement), and jargon (material in some format
  not defined here).

}

leaf: expr; equivalence; jargon; -new-notation; ad-hoc.

{ In addition, we define one ad-hoc kind of leaf, to handle
  some otherwise ill-formed formulas.
}

ad-hoc: nil.
nil: -'nil'.


{ A 'mention' formula is a basic statement with no content stroke.
  The name reflects the fact that these formulas appear (§10, §24)
  as objects of metalinguistic discussion, typically in sentences
  of the form "[formula] denotes ..." or "the abbreviated form 
  [formula] can always be replaced by the full form [formula]".

  The keyword 'expr' used here is intended to suggest reading a
  formula like "expr a" as "the expression 'a'".
}

mention: -'expr', s, leaf.

{ ................................................................
  Expressions 
}

{ Expressions are used for basic statements, function arguments,
  either side of an equivalence, and the left-hand side of a
  substitution.

  The most frequent form of expression in the book is a single-letter
  variable: upper-case Greek, lower-case italic Roman, later also
  lower-case Greek and upper-case italic.  These are often used as
  basic statements; today we would call them propositional variables.

  Bound variables are syntactically distinct from variables with
  implicit universal quantification (bound variables are Fraktur,
  others italic). We carry that distinction into the syntax here, just 
  in case we ever need it.  

  Bound variables do not, as far as I know, ever show up as basic
  statements, but I don't see anything in Frege's explanations that
  would rule it out.  He says explicitly that a variable explicitly
  bound at the root of the expression (a bound-var) is equivalent to
  an implicitly bound variable (an instance of italic or Italic).

  Some basic statements have internal structure which we need to
  capture (either to be able to process the logical formulas usefully
  or for purely typographic reasons).  So what we call leaves are not,
  strictly speaking, always leaves in OUR parse tree.

}

-expr: var; bound-var; fa.

{ Details of variables are banished down to the 'Low-level details'
  section at the bottom of the grammar. }
  
var:  Greek-letter; greek-letter; italic; Italic.

{ In the general case, the leaf expressions may come from any notation
  developed by a particular discipline.  To allow such formulas
  without changing this grammar, we provide a sort of escape hatch,
  using brackets ⦑ ... ⦒ (U+2991, U+2992, left / right angle bracket
  with dot).  For brevity, we'll call the specialized language inside
  the brackets 'jargon'. }

jargon: #2991, ~[#2991; #2992]*, #2992.


{ ................................................................
  Conditionals
}

{ §5 Conditionals are left-associative.  Since the consequent is
  always given first and the antecedent second, we could hide those
  nonterminals and just rely on the position of the child to know its
  role.  But it feels slightly less error-prone to keep the names;
  it makes a transform that shifts into conventional order easier
  to write and read.

}

conditional: consequent, s, -'if', s, antecedent.
consequent: proposition.
antecedent: prop-no-ifs.


{ ****************************************************************
  Inferences
  ****************************************************************}

{ §6 Inferences.  In the simple case we have multiple premises
  and a conclusion.  More often, one of the premises is omitted.
  (Oddly, never both premises, I do not understand why not.)

  There may be more than one inference step.
}

inference:  premises, sep,
            infstep++sep.

-premises:  -'we have:', s, premise++(sep, -'and:', s).

premise:  formula.

conclusion: formula.

{ An inference step may also refer to further premises by number.
  These are NOT given explicitly, only be reference.}

infstep: -'from which', s,
         (-'via', s, premise-references, s)?, 
         -'we infer:', s,
         (pagebreak, s)?,
         conclusion.

{ Page breaks sometimes occur after the inference line;
we encode them just after the "we infer:", but n.b.
the replacement table for the premise ref is printed after
the page break, though transcribed before it. }

pagebreak: -'|p', s, @n, s, -'|'.

{ ................................................................
  References to premises
}

{ References may refer to the first premise of Frege's modus ponens
  (the conditional) or to the second (the hypothesis).  I'll call
  these 'con' for the conditional and 'ant' for the hypothesis or
  antecedent.  If there are standard names, I don't know what they
  are.

  As far as I can see, 102 is the only formula that actually uses
  multiple premises by reference in a single inference step.  It uses
  no substitutions.  In Frege's book, then, a premise reference
  can EITHER have multiple references without substitutions or a 
  single reference with optional substitutions.

}

-premise-references: premise-ref-con; premise-ref-ant.
premise-ref-con:  -'(', s, ref++comma, s, -'):'.
premise-ref-ant:  -'(', s, ref++comma, s, -')::'.

ref: 'X'+; @n, (s, substitutions)?.

{ ................................................................
  Substitution tables
}

{ For premise references, a substitution table may be specified. }

substitutions: -'[', s, -'replacing', s, subst++sep, s, -']'.

{ A single substitution has left- and right-hand sides separated by
  'with'.  To make substitution tables easier to read and write, each
  substitution must be enclosed in parentheses.  I don't know good
  names for the two parts, so we are stuck with awkward ones.

    - oldterm, newterm
    - del, ins / delete, insert / delendum, inserendum
    - tollendum, ponendum / take, give / pull, push

  The Biblical echoes dispose me right now to take and give.  One hand
  gives and the other takes away.

}

subst: -'(', s, taken, s, -'with', s, given, s, -')'.

{ A quick survey suggests that 'taken' is always an expression
  (variable or function application), while 'given' can be arbitrarily
  complex. }

taken:  expr.
given:  proposition.


{ ****************************************************************
  Formulas (cont'd)
  ****************************************************************}

{ ................................................................
  Negation
}

{ §7 Negation }

not: -'not', s, prop-no-ifs.


{ §8 Equivalence sign.  

  It looks as if we are going to need to parse the leaves.  Frege
  refers to "Inhaltsgleichheit", which for the moment I am going to
  render as "equivalence".  In Part I, at least, the only use of
  equivalences is for variable symbols.  But in Part II, things get
  more complicated.  So we allow equivalences between parenthesized 
  propositions on the left and variables on the right.  In this case,
  Frege normally brackets the entire equivalence.

  For now (we are at the end of Part II), we do not allow
  parenthesized propositions in the right hand side, and we require
  outer brackets.  Both of those restrictions feel a little ad-hoc,
  so they may be relaxed later.

}

equivalence: simple-equiv; bracketed-equiv.

-simple-equiv: expr, s, equiv-sign, s, expr.
-bracketed-equiv: -'[', s,
                  parenthesized-prop, s, equiv-sign, s, expr,
                  s, -']'.

equiv-sign: -'≡'; -'equiv'; -'EQUIV'; -'=='.


{ ................................................................
  Functions and argument / function application
}

{ §10 Function and argument.

  Frege does not distinguish, in notation or prose, between what I
  would call "function" and "function application".  The nonterminal
  'fa' can be thought of as an abbreviation for 'function application'
  or for 'function and argument'.  

}

fa: functor, s, -'(', s, arguments, s, -')'.

{ It would feel natural to make functor an attribute, but I want the
  distinction between var and bound-var to be visible, to simplify the
  task of deciding whether to italicize or not. }

functor: var; bound-var.

-arguments: arg++comma.

arg: expr.


{ ................................................................
  Universal quantification
}

{ §11  Universal quantification. }

univ:  -'all', s, @bound-var, s, -'satisfy', s, prop-no-ifs.

bound-var: fraktur; Fraktur.


{ ****************************************************************
  Notations
  ****************************************************************}

{ §24 Elaboration of equivalence as a method of introducing a new
  notation.  In §8, Frege mentions that one reason for specifying an
  equivalence is to establish a short form to abbreviate what would
  otherwise be tedious to write out.  In §24 he gives more details. 

  1 In place of the affirmation stroke there is a double stroke, which
    Frege explains as signaling a double nature of the statement
    (synthetic on first appearance, analytic in reappearances).

  2 The proposition is an equivalence, with standard notation on the
    left and a new notation on the right.

  For purposes of data capture, we transcribe the new notation as a
  function application, in which the functor is a multi-character
  name.  For the notations used by Frege in the book, we define
  specific functors here.  As a gesture towards generality, we also
  define a generic new-notation syntax (functors beginning with
  underscore).

}

notation-declaration: -'let us denote:', s, proposition, sep,
                      -'with the expression:', s, new-notation, s,
                      right-label?.

{ When the notation declaration is actually used as a premise, it
  becomes an analytic statement and a normal kind of proposition. It
  will never be a conclusion or an axiom, only a premise. }

analytic: proposition, s, equiv-sign, s, new-notation.

{ The new notation can be known or unknown. }

new-notation: known-notation; unknown-notation.

{ A known notation is one Frege introduces. (We know it because we
  have read ahead in the book.)  We define these here for 
  convenience: better syntax checking, and the opportunity for
  custom XML representations. }

-known-notation: is-inherited
               ; follows
               ; follows-or-self
               ; unambiguous.

{ The first notation Frege defines means 'property F is 
  inherited in the f-series', where F is a unary predicate
  and f is a binary predicate such that f(x, y) means 
  that applying procedure f to x yields y.  He also wants 
  two dummy arguments with Greek letters, and from his
  examples it appears that a fifth argument is needed in 
  order to specify the order of the two greek arguments in
  the call to f().  It's possible that there are typos in
  those examples, since the order of arguments never
  varies otherwise. }
  
is-inherited: -'inherited(', s,
              property, comma,
              function, comma,
              dummy-var, comma,
              dummy-var, comma,
              order-argument, s,
              -')'.

{ Frege generally uses an uppercase letter for the property, and a
  lowercase letter for the function. But variations occur. }

property: Italic; Greek-letter; Fraktur; conditional;
          follows; follows-or-self.

function:  var.

{ Frege explains that the small greek letters are dummy variables (but
  I cannot say I understand the explanation very well. }
  
dummy-var: greek-letter.

{ If a greek letter is used for the order argument, it means that that
  is the letter given first in the call to the binary function; the
  other dummy variable comes second.  If a number is used, it means
  the first/second dummy variable is given first.  }
  
order-argument: greek-letter; '1'; '2'.


{ Frege describes the second notation as meaning 'y follows x in the
f-series'.  

I think it may be clearer to say that (x,y) is in the transitive
closure of relation f.  The conventional English term for the relation
defined here is apparently to say that y is the f-ancestor of x, which
like "ancestral" uses Frege's genealogical metaphor backwards.  }

follows: -'follows-in-seq(', s,
         (var | ^bound-var), comma,
         (var | ^bound-var), comma,
         function, comma,
         dummy-var, comma,
         dummy-var, s,
         -')'.

{ The second notation means 'y follows x in the f-series, or is the
  same as y'. }

follows-or-self: -'follows-or-same(', s,
         (var | ^bound-var), comma,
         (var | ^bound-var), comma,
         function, comma,
         dummy-var, comma,
         dummy-var, s,
         -')'.

{ The fourth notation means 'f is unambiguous', i.e. in modern terms f
  is a function. }

unambiguous: -'unambiguous(', s,
             function, comma,
             dummy-var, comma,
             dummy-var, s,
             -')'.


{ As a nod towards generality, and to enable this grammar to
  be used with other new notations, we also define a rule 
  for 'unknown' notations. For historical reasons, I'll use
  the name 'blort' to denote an unknown notation.
}

-unknown-notation: blort.

{ In kB, a blort is written like a function call in a conventional
  programming language: it has (what looks like) a function name and
  then zero or more arguments wrapped as a group in parentheses.  The
  one constraint is that the function name has to begin with an
  underscore.  For example: _foo(arg1, arg2, delta, alpha).

  For now we allow all the same kinds of arguments as in 'fa', and
  also lower-case Greek.  If more is needed, rework will be needed.

}
  
blort: @name, -'(', s, blarg**comma, -')'.

@name:  '_', [L; N; '-_.']+.

{ A blarg is (of course) an argument for a blort. Frege uses small
  Greek letters for these, as well as italics. I don't think he uses
  any upper-case Greek, but I won't rule it out. }
  
blarg:  expr; dummy-var.


{ ****************************************************************
  Low-level details
  ****************************************************************}

{ ................................................................
  Whitespace, separators
}

{ Whitespace is allowed in many places }

-s : whitespace*.
-ss: whitespace+.
-whitespace: -[#9; #A; #D; Z].

{ A 'separator' is just a place where a comma may or must occur.
  Whitespace is not allowed before the comma.  There are rules. }

-comma: -',', s.
-sep: ss; (-',', s).

-end-mark: -".".

{ ................................................................
  Variables: Greek letters
}

{ Upper-case Greek letters can be entered directly, but may also be
  spelled out. }
  
-Greek-letter: [#391 - #03A9] { 'Α'-'Ω' }
            ; -'Alpha', + #0391 {'Α'}
            ; -'Beta', + #0392 {'Β'}
            ; -'Gamma', + #0393 {'Γ'}
            ; -'Delta', + #0394 {'Δ'}
            ; -'Epsilon', + #0395 {'Ε'}
            ; -'Zeta', + #0396 {'Ζ'}
            ; -'Eta', + #0397 {'Η'}
            ; -'Theta', + #0398 {'Θ'}
            ; -'Iota', + #0399 {'Ι'}
            ; -'Kappa', + #039A {'Κ'}
            ; -'Lamda', + #039B {'Λ'}
            ; -'Lambda', + #039B {'Λ'}
            ; -'Mu', + #039C {'Μ'}
            ; -'Nu', + #039D {'Ν'}
            ; -'Xi', + #039E {'Ξ'}
            ; -'Omicron', + #039F {'Ο'}
            ; -'Pi', + #03A0 {'Π'}
            ; -'Rho', + #03A1 {'Ρ'}
            ; -'Sigma', + #03A3 {'Σ'}
            ; -'Tau', + #03A4 {'Τ'}
            ; -'Upsilon', + #03A5 {'Υ'}
            ; -'Phi', + #03A6 {'Φ'}
            ; -'Chi', + #03A7 {'Χ'}
            ; -'Psi', + #03A8 {'Ψ'}
            ; -'Omega', + #03A9 {'Ω'}
            .

{ Lower-case greek letters are allowed as arguments
  in blorts defined in a notation declaration.  With
  luck, it will be clear what they mean. }
  
-greek-letter: [#03B1 - #03C9] { 'α'-'ω' }
            ; -'alpha', + #03B1 {'α'}
            ; -'beta', + #03B2 {'β'}
            ; -'gamma', + #03B3 {'γ'}
            ; -'delta', + #03B4 {'δ'}
            ; -'epsilon', + #03B5 {'ε'}
            ; -'zeta', + #03B6 {'ζ'}
            ; -'eta', + #03B7 {'η'}
            ; -'theta', + #03B8 {'θ'}
            ; -'iota', + #03B9 {'ι'}
            ; -'kappa', + #03BA {'κ'}
            ; -'lamda', + #03BB {'λ'}
            ; -'lambda', + #03BB {'λ'}
            ; -'mu', + #03BC {'μ'}
            ; -'nu', + #03BD {'ν'}
            ; -'xi', + #03BE {'ξ'}
            ; -'omicron', + #03BF {'ο'}
            ; -'pi', + #03C0 {'π'}
            ; -'rho', + #03C1 {'ρ'}
            ; -'final-sigma', + #03C2 {'ς'}
            ; -'sigma', + #03C3 {'σ'}
            ; -'tau', + #03C4 {'τ'}
            ; -'upsilon', + #03C5 {'υ'}
            ; -'phi', + #03C6 {'φ'}
            ; -'chi', + #03C7 {'χ'}
            ; -'psi', + #03C8 {'ψ'}
            ; -'omega', + #03C9 {'ω'}
            .

{ ................................................................
  Variables: Latin letters (italics)
}

-italic: (-'*')?, ['a'-'z'].
-Italic: (-'*')?, ['A'-'Z'].

{ ................................................................
  Variables: Fraktur
}

{ I would prefer to use encoded literals for all of the following,
  but at the moment they exercise a bug in one ixml parser.  So
  for the letters I actually use in test cases, we need to use
  quoted literals instead.  This affects characters outside the
  basic multilingual plane of UCS. }
  
-fraktur: [#1D51E - #1D537]
        ; -'fa', + '𝔞' {#1D51E}
        ; -'fb', + #1D51F
        ; -'fc', + #1d520
        ; -'fd', + '𝔡' {#1d521}
        ; -'fe', + '𝔢' {#1d522}
        ; -'ff', + #1d523
        ; -'fg', + #1d524
        ; -'fh', + #1d525
        ; -'fi', + #1d526
        ; -'fj', + #1D527
        ; -'fk', + #1D528
        ; -'fl', + #1D529
        ; -'fm', + #1d52A
        ; -'fn', + #1d52B
        ; -'fo', + #1d52C
        ; -'fp', + #1d52D
        ; -'fq', + #1d52E
        ; -'fr', + #1d52F
        ; -'fs', + #1d530
        ; -'ft', + #1d531
        ; -'fu', + #1d532
        ; -'fv', + #1d533
        ; -'fw', + #1d534
        ; -'fx', + #1d535
        ; -'fy', + #1d536
        ; -'fz', + #1d537
        .

-Fraktur: [#1d504 - #1d51d] { not all letters are present! }
        ; -'FA', + #1D504 {'𝔄'}
        ; -'FB', + #1D505 {'𝔅'}
        ; -'FC', + #1D506 {𝔆}
        ; -'FD', + #1D507 {𝔇}
        ; -'FE', + #1D508 {𝔈}
        ; -'FF', + "𝔉" {#1D509} {𝔉}
        ; -'FG', + #1D50A {𝔊}
        ; -'FH', + #1D50B {𝔈}
        ; -'FI', + #1D50C {𝔌}
        ; -'FJ', + #1D50D {𝔍}
        ; -'FK', + #1D50E {𝔎}
        ; -'FL', + #1D50F {𝔏}
        ; -'FM', + #1D510 {𝔐}
        ; -'FN', + #1D511 {𝔑}
        ; -'FO', + #1D512 {𝔒}
        ; -'FP', + #1D513 {𝔓}
        ; -'FQ', + #1D514 {𝔔}
        ; -'FR', + #1D515 {𝔕}
        ; -'FS', + #1D516 {𝔖}
        ; -'FT', + #1D517 {𝔗}
        ; -'FU', + #1D518 {𝔘}
        ; -'FV', + #1D519 {𝔙}
        ; -'FW', + #1D51A {𝔚}
        ; -'FX', + #1D51B {𝔛}
        ; -'FY', + #1D51C {𝔜}
        ; -'FZ', + #1D51D {𝔝}
        .

References

[Angelleli 1964] Angelleli, Ignacio, ed. Frege, Gottlob. Begriffsschrift und andere Aufsätze. Zweite Auflage mit E. Husserls und H. Scholz’ Anmerkungen. Hildesheim: Georg Olms, 1964. (See also Frege 1879.)

[Cook 2023] Cook, Roy. Frege’s Logic in The Stanford Encyclopedia of Philosophy (Spring 2023 Edition), ed. Edward N. Zalta and Uri Nodelman. On the web at <https://plato.stanford.edu/archives/spr2023/entries/frege-logic/>

[Dockrey 2019] Dockrey, Matthew. Gottlob. Web site: <https://www.attoparsec.com/artifacts/gottlob/begriffsschrift.html>

[Dunning 2020] Dunning, David E. ‘Always mixed together’: Notation, language, and the pedagogy of Frege’s Begriffsschrift. Modern Intellectual History 17.4 (December 2020): 1099-1131. doi:https://doi.org/10.1017/S1479244318000410. On the web at <https://www.cambridge.org/core/journals/modern-intellectual-history/article/abs/always-mixed-together-notation-language-and-the-pedagogy-of-freges-begriffsschrift/1A2921F99668935D917290DFBFE9C102#access-block> and (perhaps a preprint?) <https://ora.ox.ac.uk/objects/uuid:011a51fb-4f0a-46f3-8e2f-85d23a798567/download_file?file_format=application%2Fpdf&safe_filename=Dunning_2018_Always_mixed_together.pdf&type_of_work=Journal+article>

[Frege 1879] Frege, Gottlob. Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. (Concept writing: a formula language for pure thought modeled on that of arithmetic.) Halle a.S.: Louis Nebert, 1879. (See also Angelelli 1964.) A scan of the book is available in Gallica, the online presence of the Bibliothèque nationale de France (BNF), at https://gallica.bnf.fr/ark:/12148/bpt6k65658c

[Frege 1893] Frege, G[ottlob]. Grundgesetze der Arithmetic: begriffsschriftlich abgeleitet. (Basic laws of arithmetic: derived using concept writing.) 2 volumes. Jena: Verlag von Hermann Pohle, 1893, 1903. Rpt. with additions by Christian Thiel, Hildesheim et al.: Georg Olms, 2009. A scan of the book (at least volume I) is available in Gallica, the online presence of the Bibliothèque nationale de France (BNF), at https://gallica.bnf.fr/ark:/12148/bpt6k77790t/

[IDPF/W3C 2019] International Digital Publishing Forum and World Wide Web Consortium (W3C). Epub 3.2. Final Community Group Specification 08 May 2019. On the web at https://www.w3.org/publishing/epub3/epub-spec.html

[Pamp 2012] Pamp, Quirin. frege – Typeset fregean Begriffsschrift (TeX macro package). Version 1.3, 2012. On the Web at https://www.ctan.org/pkg/frege

[Parsons 2005] Parsons, Josh. begriff – Typeset Begriffschrift (TeX macro package). Version 1.6, 2005. On the Web at https://www.ctan.org/pkg/begriff

[Pemberton 2013] Pemberton, Steven. Invisible XML. Presented at Balisage: The Markup Conference 2013, Montréal, Canada, August 6 - 9, 2013. In Proceedings of Balisage: The Markup Conference 2013. Balisage Series on Markup Technologies, vol. 10 (2013). doi:https://doi.org/10.4242/BalisageVol10.Pemberton01.

[Pemberton 2021] Pemberton, Steven. Invisible XML Specification (Draft). 2021-01-28. On the Web at https://invisiblexml.org/ixml-specification.html

[Rossberg 2021] Rossberg, Marcus. Grundgesetze.sty for LaTeX2e Documentation. Version 1.03 (26 April 2021). The package is on the Web at <ctan>; the documentation is also on the Web, at <https://mirror.mwt.me/ctan/macros/latex/contrib/grundgesetze/grundgesetze.pdf>.

[Russell / Whitehead 1910-1913] Whitehead, Alfred North, and Bertrand Russell, Principia mathematica 3 volumes, (Cambridge: Cambridge University Press, 1910, 1912, 1913).

[Schlimm 2018] Schlimm, Dirk. On Frege’s Begriffsschrift Notation for Propositional Logic: Design Principles and Trade-Offs. History and Philosophy of Logic 39.1 (2018): 53-79. doi:https://doi.org/10.1080/01445340.2017.1317429. On the Web at https://www.tandfonline.com/doi/full/10.1080/01445340.2017.1317429?needAccess=true and (as preprint) at https://www.cs.mcgill.ca/~dirk/schlimm2017-begriffsschrift-prefinal.pdf

[Sutcliffe 2022] Sutcliffe, G. The Logic Languages of the TPTP World. Logic Journal of the IGPL 2022, jzac068. doi:https://doi.org/10.1093/jigpal/jzac068.

[Sutcliffe/Suttner 2022] Sutcliffe, Geoff, and Christian Suttner. The TPTP Problem Library for Automated Theorem Proving. Release TPTP-v8.1.2. On the web at https://tptp.org/

[Temkin 2019] Temkin, Daniel. Gottlob: Write Code in Frege’s Concept Notation. Blog post on the site Esoteric.Codes. On the Web at: <https://esoteric.codes/blog/gottlob-write-code-in-freges-concept-notation> .

[Wermuth 2015] Wermuth, Udo. Typesetting the “Begriffsschrift” by Gottlob Frege in plain TeX. TUGboat 36.3 (2015): 243-256.


[1] I am grateful to Deborah Aleyne Lapeyre and Claus Huitfeldt for encouragement and discussion; some of the more insightful remarks in this paper I owe to them.

[2] The attentive reader will note that if scanned images of Frege 1879 are available, a usable electronic text ought to be just a matter of optical character recognition and cleanup. True. And indeed, the Bibliothèque nationale has already performed OCR on its scan. The results show why this approach does not pan out well. Not only is the OCR engine deeply confused by the formulas, but the quality issues in the scan reduce the quality of the OCR. The BN estimates that 74.44% of the characters in the document have been recognized correctly. Simple tests show that it is faster to type the text in twice and compare the two icopies to find errors than to work through the BN’s OCR text correcting errors.

[3] Clearer renderings of the formulas are available in more recent reprints, but those reprints appear to be protected by copyright.

[4] If the only goal were to produce printed pages or PDF, it would not be essential that the digital form of the book be XML; the book could be transcribed in TeX and the macros developed by Udo Wermuth (Wermuth 2015) or others could be used to lay out the formulas. But the goal is not a printed book or a digital representation of an imaginary printed book. The goal is electronic book in EPub format which is trying to be an electronic book in EPub format, not trying to be a printed book. That requires XML.

It would be possible to create an ebook without making the XML representations of Frege’s formulas be TEI-compatible, but given the human resources available for the work, TEI compatibility is highly desirable.

[5] Easy to keyboard, that is, compared to entering the appropriate XML directly.

[6] The notation used in his 1893 work differs in some details (see Wermuth 2015); whether those changes are minor or not is a topic of some philosophical discussion (see Cook 2023).

[7] For simplicity, I will call them propositions in what follows, ignoring the warnings of careful philosophers who caution that what Frege calls judgeable content may not be precisely the same as a proposition, in ways that they do not explain.

[8] A note on typographic terminology seems unavoidable here. Frege refers to Latin letters and German letters, as shorthand for letters printed using the Antiqua fonts customary in Germany for printing Latin texts (and foreign words in German texts) on the one hand, and on the other letters printed using Fraktur, customarily reserved for works in German. Similar distinctions are in principle possible when writing by hand, although experience shows that contemporary German students confronted with a carefully formed letter a in a traditional German hand are not guaranteed to have any idea what letter it represents.

I speak simply of letters written in Fraktur, although Frege’s term German letter and the related German script generally cover both Fraktur and other angular fonts (gebrochene Schriftarten) like textura, rotunda, and Schwabacher. Both the typographic practice of Frege’s publishers and the practice of mathematicians make clear that by German letter Frege meant letter printed in Fraktur.

[9] It should be admitted that this is the longest formula in the book, and given in this form only as an example of the effect of substitution of terms.

[10] The asterisk may be unnecessary, but the author got cold feet over possible conflicts.

[11] For example, all variables (including free ones) are rendered in Fraktur, ignoring Frege’s careful typographic distinction between bound variables with an explicitly delimited scope (rendered in Fraktur) and unbound variables for which an implicit universal quantification is assumed (rendered in italic). The designer of the programming language also appears either to have misunderstood Frege’s notation for material implication or to have trouble expressing it clearly in prose.

[12] Since the English translation was published in 2013, however, it appears that the translators were less daunted by these macros than I am. Over the 500-odd pages of the Grundgesetze, they will have transcribed thousands of formulas using this notation.

[13] The resulting SVG would be more elegant if identical subexpressions were defined only once, but the current implementation makes no attempt to avoid duplication of definitions: each occurrence of a repeating subexpression gets its own definition.

[14] The renderings of Frege’s formulas into conventional notation given above were all generated using an XSLT stylesheet constructed for the purpose, since attempts to do the job manually ran into too many errors with parentheses.

[15] The author thanks Lynne Price for her years of effort trying to lead me to comprehend the benefits of deeply nested markup as a motivation for the tag minimization features of SGML.

[16] It is a corollary of Goldfarb’s Law, however, that such troubles can only be minimized, not eliminated entirely.)

C. M. Sperberg-McQueen

Founder and principal

Black Mesa Technologies LLC

C. M. Sperberg-McQueen is the founder and principal of Black Mesa Technologies, a consultancy specializing in helping memory institutions improve the long term preservation of and access to the information for which they are responsible.

He served as editor in chief of the TEI Guidelines from 1988 to 2000, and has also served as co-editor of the World Wide Web Consortium’s XML 1.0 and XML Schema 1.1 specifications.